练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知M是圆周上的一个定点，若在圆周上任取一点N，连接MN，则弦MN的长不小于圆半径的概率是（　　）
    A．$\frac{1}{4}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．$\frac{2}{3}$

    分析 根据已知中A是圆上固定的一定点，在圆上其他位置任取一点B，连接A、B两点，它是一条弦，我们求出B点位置所有基本事件对应的弧长，及满足条件AB长大于半径的基本事件对应的弧长，代入几何概型概率计算公式，即可得到答案

    解答 解：在圆上其他位置任取一点N，设圆半径为R，
    则N点位置所有情况对应的弧长为圆的周长2πR，
    其中满足条件MN的长度不小于半径长度的对应的弧长为 $\frac{2}{3}$•2πR，
    则AB弦的长度大于等于半径长度的概率P=$\frac{\frac{2}{3}•2πR}{2πR}=\frac{2}{3}$；
    故选D．

    点评 本题考查的知识点是几何概型，其中根据已知条件计算出所有基本事件对应的几何量及满足条件的基本事件对应的几何量是解答的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    17．若定义在R上的函数$f（x）={log_3}（{2x+\sqrt{4{x^2}+a}}）$为奇函数，则实数a的值为（　　）
    A．-1B．0C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=2lnx+x2-ax，a∈R．
    （1）若函数y=f（x）在（0，+∞）上单调递增，求实数a的取值范围；
    （2）若a=e，解不等式：f（x）＜2；
    （3）求证：当a＞4时，函数y=f（x）只有一个零点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．记函数y=ex在x=n（n=1，2，3，…）处的切线为ln．若切线ln与ln+1的交点坐标为（An，Bn），那么（　　）
    A．数列{An}是等差数列，数列{Bn}是等比数列
    B．数列{An}与{Bn}都是等差数列
    C．数列{An}是等比数列，数列{Bn}是等差数列
    D．数列{An}与{Bn}都是等比数列

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．将函数y=sin（2x+$\frac{π}{6}$）图象上的点M（θ，$\frac{\sqrt{3}}{2}$）（0＜θ＜$\frac{π}{4}$）向右平移t（t＞0）个单位长度得到点M′．若M′位于函数y=sin2x的图象上，则（　　）
    A．θ=$\frac{π}{12}$，t的最小值为$\frac{π}{12}$B．θ=$\frac{π}{12}$，t的最小值为$\frac{π}{6}$
    C．θ=$\frac{π}{6}$，t的最小值为$\frac{π}{6}$D．θ=$\frac{π}{6}$，t的最小值为$\frac{π}{12}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．在实数集R中定义一种运算“*”，对任意给定的a，b∈R，a*b为唯一确定的实数，且具有性质：
    （1）对任意a，b∈R，a*b=b*a；（2）对任意a∈R，a*0=a；（3）对任意a，b∈R，（a*b）*c=c*（ab）+（a*c）+（c*b）-2c．关于函数f（x）=（3x）*$\frac{1}{3x}$的性质，有如下说法：
    ①函数f（x）的最小值为3；
    ②函数f（x）为奇函数；
    ③函数f（x）的单调递增区间为（-∞，-$\frac{1}{3}$），（$\frac{1}{3}$，+∞）．
    其中所有正确说法的个数为（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知F1，F2分别是椭圆mx2+y2=m（0＜m＜1）的左、右焦点，P为椭圆上任意一点，若$\frac{|\overrightarrow{P{F}_{2}}{|}^{2}+|\overrightarrow{P{F}_{1}}|}{|\overrightarrow{P{F}_{1}}|}$的最小值为$\frac{4}{3}$，则椭圆的离心率是（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{1}{4}$D．$\frac{1}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数f（x）=2alnx+x2-（a+4）x+1（a为常数）
    （1）若a＞0，讨论f（x）的单调性；
    （2）若对任意的 a∈（1，$\sqrt{2}$），都存在 x0∈（3，4]使得不等式f（x0）+ln a+1＞m（a-a2）+2a ln$\frac{4}{e}$成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

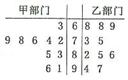    17．渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩（单位：分）数据的茎叶图如图所示．
    （1）若公司决定测试成绩高于85分的员工获得“职业技能好能手”称号，求从这20名员工中任选三人，其中恰有两人获得“职业技能好能手”的概率；
    （2）公司结合这次测试成绩对员工的绩效奖金进行调整（绩效奖金方案如表），若以甲部门这10人的样本数据来估计该部门总体数据，且以频率估计概率，从甲部门所有员工中任选3名员工，记绩效奖金不小于3a的人数为ξ，求ξ的分布列及数学期望．
     分数[60，70）[70，80）[80，90）[90，100]
     奖金 a 2a 3a 4a

    查看答案和解析>>

    同步练习册答案