
分析 (1)求出原函数的导函数,求得导函数的零点,然后对a分类求出函数的单调区间.
(2)由(1)可知,f(x)在(3,4]上单调递增.求出f(x)在(3,4]上的最大值,把问题转化为f(x)max+lna+1>$m(a-{a}^{2})+2aln\frac{4}{e}$,即2-2a+lna>m(a-a2)恒成立.即对任意的a∈(1,$\sqrt{2}$),不等式lna+ma2-(m+2)a+2>0恒成立.设h(a)=lna+ma2-(m+2)a+2,然后分m≥1和m<1讨论a∈(1,$\sqrt{2}$)时h(a)>0是否恒成立求得实数m的取值范围.
解答 解:(1)f′(x)=$\frac{2a}{x}+2x-(a+4)=\frac{(x-2)(2x-a)}{x}$.
令f′(x)=0,得x1=2,${x}_{2}=\frac{a}{2}$.
①当a>4时,$\frac{a}{2}$>2,当2<x<$\frac{a}{2}$时,f′(x)<0;当0<x<2时,f′(x)>0.
此时f(x)的单调增区间为(0,2),($\frac{a}{2},+∞$),单调递减区间为(2,$\frac{a}{2}$).
②当a=4时,$\frac{a}{2}$=2,f′(x)=$\frac{2(x-2)^{2}}{x}≥$0,f(x)在(0,+∞)上单调递增.
③当0<a<4时,$\frac{a}{2}$<2,当$\frac{a}{2}$<x<2时,f′(x)<0;当0<x<$\frac{a}{2}$或x>2时,f′(x)>0.
此时f(x)的单调增区间为(0,$\frac{a}{2}$),(2,+∞),单调递减区间为($\frac{a}{2}$,2).
综上所述,当a>4时,f(x)的单调增区间为(0,2),($\frac{a}{2},+∞$),单调递减区间为(2,$\frac{a}{2}$).
当a=4时,f(x)在(0,+∞)上单调递增.
当0<a<4时,f(x)的单调增区间为(0,$\frac{a}{2}$),(2,+∞),单调递减区间为($\frac{a}{2}$,2).
(2)由(1)可知,当a∈(1,$\sqrt{2}$)时,f(x)在(3,4]上单调递增.
∴x∈(3,4]时,f(x)max=f(4)=4aln2-4a+1,依题意,
只需f(x)max+lna+1>$m(a-{a}^{2})+2aln\frac{4}{e}$,即2-2a+lna>m(a-a2)恒成立.
即对任意的a∈(1,$\sqrt{2}$),不等式lna+ma2-(m+2)a+2>0恒成立.
设h(a)=lna+ma2-(m+2)a+2,则h(1)=0.
$h′(a)=\frac{1}{a}+2ma-(m+2)=\frac{(2a-1)(ma-1)}{a}$.
∵a∈(1,$\sqrt{2}$),∴$\frac{2a-1}{a}$>0.
①当m≥1时,对任意的a∈(1,$\sqrt{2}$),ma-1>0,∴h′(a)>0,h(a)在(1,$\sqrt{2}$)上单调递增,h(a)>h(1)=0恒成立;
②当m<1时,存在a0∈(1,$\sqrt{2}$),使得当a∈(1,a0)时,ma-1<0,∴h′(a)<0,h(a)单调递减,h(a)<h(1)=0,
∴a∈(1,$\sqrt{2}$)时,h(a)>0不能恒成立.
综上述,实数m的取值范围是[1,+∞).
点评 本题考查利用导数研究函数的单调性,考查了利用导数求函数的最值,考查分类讨论的数学思想方法和数学转化思想方法,是压轴题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f($\frac{π}{6}$)>$\sqrt{2}$f($\frac{π}{4}$) | B. | $\sqrt{2}$sin1•f(1)>f($\frac{π}{4}$) | C. | f($\frac{π}{6}$)>$\sqrt{3}$f($\frac{π}{3}$) | D. | $\sqrt{2}$f($\frac{π}{4}$)>$\sqrt{3}$f($\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2,4} | B. | {0,1,2} | C. | {1,4} | D. | {0,1,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 60 | C. | 80 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
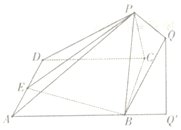 已知如图所示的几何体中,四边形ABCD是边长为2的菱形,面PBC⊥面A BCD,点E是AD 的中点,PQ∥面ABCD且点Q在面ABCD上的射影Q′落在AB的延长线上,若PQ=1,PB=$\sqrt{2}$,且($\overrightarrow{PB}+\overrightarrow{PC}$)•$\overrightarrow{BC}$=0,$\overrightarrow{AB}•\overrightarrow{AD}$=2
已知如图所示的几何体中,四边形ABCD是边长为2的菱形,面PBC⊥面A BCD,点E是AD 的中点,PQ∥面ABCD且点Q在面ABCD上的射影Q′落在AB的延长线上,若PQ=1,PB=$\sqrt{2}$,且($\overrightarrow{PB}+\overrightarrow{PC}$)•$\overrightarrow{BC}$=0,$\overrightarrow{AB}•\overrightarrow{AD}$=2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com