
| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |
分析 根据题意,利用奇函数的性质可得f(0)=log2(1)+20-a=0,解可得a=1,即可得函数f(x)的解析式,结合指数函数与对数函数的性质分析可得函数f(x)在[0,+∞)上为增函数,结合函数的奇偶性可得函数f(x)在R上为增函数,由此可以将f(x2-3x-1)+9<0转化为x2-3x+2<0,解可得x的取值范围,即可得答案.
解答 解:函数f(x)是定义域为R的奇函数,则有f(0)=0,
即f(0)=log2(1)+20-a=0,
解可得a=1,
则当x≥0时,f(x)=log2(x+1)+2x-1,
则有f(3)=log2(4)+23-1=9,
又由当x≥0时,f(x)=log2(x+1)+2x-1,而函数y=log2(x+1)和函数y=2x-1都是增函数,则函数f(x)在[0,+∞)上为增函数,
又由函数f(x)是定义域为R的奇函数,则在区间(-∞,0]上也是增函数,
故函数f(x)在R上为增函数,
f(x2-3x-1)+9<0⇒f(x2-3x-1)+f(3)<0⇒f(x2-3x-1)<-f(3)⇒f(x2-3x-1)<f(-3)⇒x2-3x-1<-3⇒x2-3x+2<0,
解可得:-1<x<2,
即x的取值范围为(-1,2);
故选:D.
点评 本题考查函数奇偶性与单调性的综合应用,关键是利用函数的奇偶性求出a的值.


科目:高中数学 来源: 题型:解答题
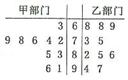 渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩(单位:分)数据的茎叶图如图所示.
渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩(单位:分)数据的茎叶图如图所示.| 分数 | [60,70) | [70,80) | [80,90) | [90,100] |
| 奖金 | a | 2a | 3a | 4a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | -i | D. | i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
| 男生 | 女生 | 合计 | |
| 优秀 | |||
| 非优秀 | |||
| 合计 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com