
分析 (1)联立方程组,能求出l1,l2的交点.
(2)( i)当直线ax+2y-6=0过l1与l2的交点P时,不能构成三角形,当直线ax+2y-6=0分别与l1、l2时,不能构成三角形,由此能求出结果.
(3)若所求直线斜率存在,设所求的直线方程为y-1=k(x+2),由所求的直线与点A(-1,-2)的距离为1,利用点到直线距离公式求出$k=-\frac{4}{3}$,从而求出直线l的方程;若所求直线斜率不存在时,即l为x+2=0,满足题意.由此能求出直线l的方程.
解答 解:(1)由$\left\{\begin{array}{l}x-2y+4=0\\ 4x+3y+5=0\end{array}\right.⇒\left\{\begin{array}{l}x=-2\\ y=1\end{array}\right.$…(2分)
∴l1,l2的交点为P(-2,1).…(3分)
(2)( i)当直线ax+2y-6=0过l1与l2的交点P时,不能构成三角形,
∴a•(-2)+2×1-6≠0,解得a≠-2,…(5分)
( ii)当直线ax+2y-6=0分别与l1、l2时,不能构成三角形,
∴$a≠-1,且a≠\frac{8}{3}$
综上所述:$a≠-2,且a≠-1,且a≠\frac{8}{3}$.…(9分)
(3)若所求直线斜率存在,
设所求的直线方程为y-1=k(x+2),即kx-y+(2k+1)=0
∵所求的直线与点A(-1,-2)的距离为1,$\frac{{|{-k+2+2k+1}|}}{{\sqrt{{k^2}+1}}}=1$,得$k=-\frac{4}{3}$…(11分)
即所求的直线l的方程为4x+3y+5=0…(12分)
若所求直线斜率不存在时,即l为x+2=0,
∵点A(-1,-2)到直线l为x+2=0的距离为1,
∴直线x+2=0也满足题意.…(15分)
故所求的直线l的方程为4x+3y+5=0,或x+2=0.…(16分)
点评 本题考查两直线交点坐标的求法,考查实数满足的条件的求法,考查直线方程的求法,涉及到直线方程等基础知识,考查运算求解能力,考查化归与转化思想,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 60 | C. | 80 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
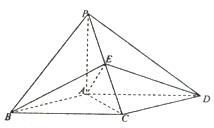 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 原点轴对称 | B. | x轴对称 | C. | y轴对称 | D. | y=x对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | a>b>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com