
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
分析 设三支款式相同、颜色不同的圆珠笔分别为A,B,C,与之相同颜色的笔帽分别为a,b,c,利用列举法求出将笔和笔帽随机套在一起,基本事件有6个,小王将两支笔和笔帽的颜色混搭包含的基本事件有3个,由此能求出小王将两支笔和笔帽的颜色混搭的概率.
解答 解:设三支款式相同、颜色不同的圆珠笔分别为A,B,C,与之相同颜色的笔帽分别为a,b,c,
将笔和笔帽随机套在一起,基本事件有:
(Aa,Bb,Cc),(Aa,Bc,cB),(Ab,Ba,Cc),(Ab,Bc,Ca),(Ac,Bb,Ca),(Ac,Ba,Cb),共有6个基本事件,
小王将两支笔和笔帽的颜色混搭包含的基本事件有:
(Aa,Bc,cB),(Ab,Ba,Cc),(Ac,Bb,Ca),共有3个基本事件,
∴小王将两支笔和笔帽的颜色混搭的概率是p=$\frac{3}{6}=\frac{1}{2}$.
故选:C.
点评 本题考查概率的求法,涉及到古典概型、列举法等基础知识,考查推理论证能力、运算求解能力、数据处理能力,考查数形结合思想、集合思想,是基础题.


 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:选择题
| A. | f($\frac{π}{6}$)>$\sqrt{2}$f($\frac{π}{4}$) | B. | $\sqrt{2}$sin1•f(1)>f($\frac{π}{4}$) | C. | f($\frac{π}{6}$)>$\sqrt{3}$f($\frac{π}{3}$) | D. | $\sqrt{2}$f($\frac{π}{4}$)>$\sqrt{3}$f($\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
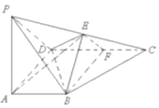 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
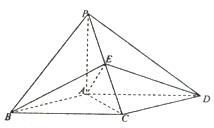 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 人数 x y | A | B | C |
| A | 14 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 原点轴对称 | B. | x轴对称 | C. | y轴对称 | D. | y=x对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
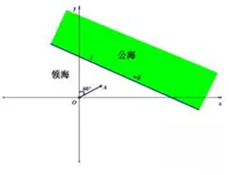 如图,已知直线l:x+$\sqrt{3}$y-c=0(c>0)为公海与领海的分界线,一艘巡逻艇在O处发现了北偏东60°海面上A处有一艘走私船,走私船正向停泊在公海上接应的走私海轮B航行,以使上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,且两者都是沿直线航行,但走私船可能向任一方向逃窜.
如图,已知直线l:x+$\sqrt{3}$y-c=0(c>0)为公海与领海的分界线,一艘巡逻艇在O处发现了北偏东60°海面上A处有一艘走私船,走私船正向停泊在公海上接应的走私海轮B航行,以使上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,且两者都是沿直线航行,但走私船可能向任一方向逃窜.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com