
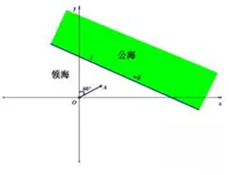
 ��ͼ����ֱ֪��l��x+$\sqrt{3}$y-c=0��c��0��Ϊ�������캣�ķֽ��ߣ�һ��Ѳ��ͧ��O�������˱�ƫ��60�㺣����A����һ����˽������˽������ͣ���ڹ����Ͻ�Ӧ����˽����B���У���ʹ�Ϻ��ֺ��Ӵܣ���֪Ѳ��ͧ�ĺ�������˽�����ٵ�2���������߶�����ֱ�ߺ��У�����˽����������һ�����Ӵܣ�
��ͼ����ֱ֪��l��x+$\sqrt{3}$y-c=0��c��0��Ϊ�������캣�ķֽ��ߣ�һ��Ѳ��ͧ��O�������˱�ƫ��60�㺣����A����һ����˽������˽������ͣ���ڹ����Ͻ�Ӧ����˽����B���У���ʹ�Ϻ��ֺ��Ӵܣ���֪Ѳ��ͧ�ĺ�������˽�����ٵ�2���������߶�����ֱ�ߺ��У�����˽����������һ�����Ӵܣ����� ��1����ػ��ΪP��x��y��������|OP|=2|AP|�з��̻��ɣ�
��2����|OA|=t������ػ��켣���̣�����ֱ����Բ���ཻ�в���ʽ�ó�t�ķ�Χ���ɵó�|OA|�����ֵ��
��� �⣺��1��������֪��A��3$\sqrt{3}$��3��������˽���ܱ��ػ�ĵ�ΪP��x��y����
��|OP|=2|AP|��
��$\sqrt{{x}^{2}+{y}^{2}}$=2$\sqrt{��x-3\sqrt{3}��^{2}+��y-3��^{2}}$���������x-4$\sqrt{3}$��2+��y-4��2=16��
����˽���ܱ��ػ�ĵ�Ĺ켣���ԣ�4$\sqrt{3}$��4��ΪԲ�ģ���4Ϊ�뾶��Բ��
��2���������$\frac{c}{2}$=20����c=40����ֱ��l�ķ���Ϊx+$\sqrt{3}$y-40=0��
��|OA|=t����A��$\frac{\sqrt{3}}{2}$t��$\frac{1}{2}$t����t��0����
����˽���ܱ��ػ�ĵ�ΪP��x��y������|OP|=2|AP|��
��$\sqrt{{x}^{2}+{y}^{2}}$=2$\sqrt{��x-\frac{\sqrt{3}}{2}t��^{2}+��y-\frac{1}{2}t��^{2}}$��
�������x-$\frac{2\sqrt{3}}{3}$t��2+��y-$\frac{2}{3}$t��2=$\frac{4}{9}{t}^{2}$��
����˽���ܱ��ػ�ĵ�Ĺ켣����C��$\frac{2\sqrt{3}}{3}$t��$\frac{2}{3}t$��ΪԲ�ģ���$\frac{2}{3}t$Ϊ�뾶��Բ��
����֤���캣�ڲ�����˽������Բ��C��ֱ��l�ľ���d��$\frac{2}{3}t$��
��$\frac{|\frac{2\sqrt{3}}{3}t+\frac{2\sqrt{3}}{3}t-40|}{2}$��$\frac{2}{3}$t��
��ã�t��$\frac{30}{\sqrt{3}+1}$=15��$\sqrt{3}$-1����
��O��A֮�����Զ������15��$\sqrt{3}$-1�����
���� ���⿼���˹켣���̵���⣬ֱ����Բ��λ�ù�ϵ�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{5}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
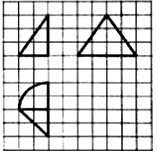
| A�� | 2+�� | B�� | 2+4�� | C�� | 6+�� | D�� | 6+4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com