
分析 先根据A∩B是一个单元素集合,得到直线和抛物线相切,得到a2+b2=1,结合图象得到集合P的面积=半径为1小圆的面积+半径为2大圆的面积的$\frac{1}{4}$,问题得以解决
解答 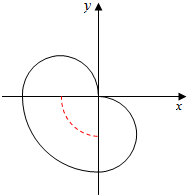 解:集合A={(x,y)|y=x2+2bx+1},B={(x,y)|y=2a(x+b)},且A∩B是一个单元素集合,
解:集合A={(x,y)|y=x2+2bx+1},B={(x,y)|y=2a(x+b)},且A∩B是一个单元素集合,
∴直线和抛物线相切,
∴由x2+2bx+1=2a(x+b),即x2+2(b-a)x+1-2ab=0,有相等的实根,所以△=0即a2+b2=1,
∵存在a<0,b<0,P={(x,y)|(x-a)2+(y-b)2≤1},
∴圆心在以原点为圆心,以1为半径的圆上的一部分(第三象限)
∴如图所示,集合P中圆的边界的移动是半径为1的圆的边界的移动就是沿着那个半径为2的那个$\frac{1}{4}$圆弧上,
∴集合P的面积=半径为1小圆的面积+半径为2大圆的面积的$\frac{1}{4}$,
∴集合C的面积=π+π=2π,
故答案为:2π.
点评 本题考查了直线和抛物线的位置关系,以及集合与集合的关系,关键是画出图形.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:解答题
| 人数 x y | A | B | C |
| A | 14 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
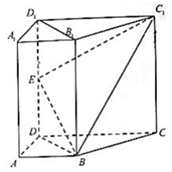 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
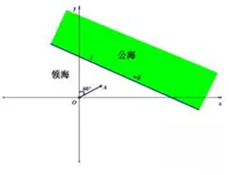 如图,已知直线l:x+$\sqrt{3}$y-c=0(c>0)为公海与领海的分界线,一艘巡逻艇在O处发现了北偏东60°海面上A处有一艘走私船,走私船正向停泊在公海上接应的走私海轮B航行,以使上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,且两者都是沿直线航行,但走私船可能向任一方向逃窜.
如图,已知直线l:x+$\sqrt{3}$y-c=0(c>0)为公海与领海的分界线,一艘巡逻艇在O处发现了北偏东60°海面上A处有一艘走私船,走私船正向停泊在公海上接应的走私海轮B航行,以使上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,且两者都是沿直线航行,但走私船可能向任一方向逃窜.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
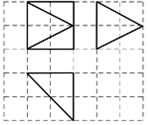 如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )
如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com