练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为（　　）
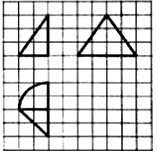
    A．2+πB．2+4πC．6+πD．6+4π

    分析 首先还原几何体为$\frac{1}{4}$圆锥与三棱锥的组合体，然后计算体积．

    解答 解：由三视图得到几何体为$\frac{1}{4}$圆锥与三棱锥的组合体，圆锥底面半径为2，三棱锥是底面为腰长为2 的等腰直角三角形，高为3，如图
    所以几何体的体积为：$\frac{1}{4}×\frac{1}{3}π×{2}^{2}×3+\frac{1}{3}×\frac{1}{2}×2×2×3$=π+2；
    故选A．

    点评 本题考查了由几何体的三视图求几何体的体积；关键是正确还原几何体，根据图中数据求体积．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

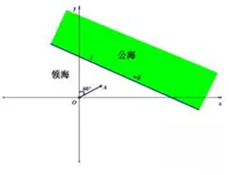    11．如图，已知直线l：x+$\sqrt{3}$y-c=0（c＞0）为公海与领海的分界线，一艘巡逻艇在O处发现了北偏东60°海面上A处有一艘走私船，走私船正向停泊在公海上接应的走私海轮B航行，以使上海轮后逃窜．已知巡逻艇的航速是走私船航速的2倍，且两者都是沿直线航行，但走私船可能向任一方向逃窜．
    （1）如果走私船和巡逻船相距6海里，求走私船能被截获的点的轨迹；
    （2）若O与公海的最近距离20海里，要保证在领海内捕获走私船（即不能截获走私船的区域与公海不想交）．则O，A之间的最远距离是多少海里？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．有下列一列数：1，8，27，64，      ，216，343，…，按照此规律，横线中的数应为（　　）
    A．75B．100C．125D．150

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知服从正态分布N（μ，σ2）的随机变量，在区间（μ-σ，μ+σ），（μ-2σ，μ+2σ）和（μ-3σ，μ+3σ）内取值的概率分别为68.27%，95.45%和99.73%，某中学为10000名员工定制校服，设学生的身高（单位：cm）服从正态分布N（173，25），则适合身高在158～188cm范围内学生穿的校服大约要定制9973套．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

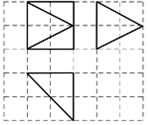    3．如图，网格纸上小正方形的边长为a，粗实线画出的是某多面体的三视图，此几何体的表面积为$12+4（\sqrt{2}+\sqrt{5}）$，则实数a=（　　）
    A．1B．2C．$\sqrt{2}$D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．若函数f（x）=ax2+（a2+1）x-a（a＞0）的一个零点为x0，则x0的最大值为$\sqrt{2}$-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．在坐标平面xOy内，O为原点，点$P（\frac{{\sqrt{3}}}{2}，\frac{1}{2}）$，射线OP逆时针旋转$\frac{π}{2}$，则旋转后的点P坐标为（-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．设（2x-1）4=a0+a1x+a2x2+a3x3+a4x4
    （1）求a2的值
    （2）求（a0+a2+a4）2-（a1+a3）2的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．下列命题中正确命题的个数是（　　）
    （1）对于命题p：?x∈R，使得x2+x+1＜0，则￢p：?x∈R，均有x2+x+1＞0；
    （2）命题“已知x，y∈R，若x+y≠3，则x≠2或y≠1”是真命题；
    （3）回归直线的斜率的估计值为1.23，样本点的中心为（4，5），则回归直线方程为$\widehat{y}$=1.23x+0.08；
    （4）m=3是直线（m+3）x+my-2=0与直线mx-6y+5=0互相垂直的充要条件．
    A．1B．3C．2D．4

    查看答案和解析>>

    同步练习册答案