
分析 根据题意画出图形,结合图形,利用单位圆和三角函数,
即可求出旋转后的点P坐标.
解答 解:如图所示,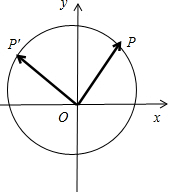
坐标平面xOy内,点$P(\frac{{\sqrt{3}}}{2},\frac{1}{2})$,
则P(cos$\frac{π}{6}$,sin$\frac{π}{6}$);
射线OP逆时针旋转$\frac{π}{2}$,得P′(cos$\frac{2π}{3}$,sin$\frac{2π}{3}$),
即P′(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
∴旋转后的点P坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
故答案为:$(-\frac{1}{2},\frac{{\sqrt{3}}}{2})$.
点评 本题考查了向量旋转的应用问题,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 1 | 2 | 3 | 4 | …第一行 |
| 2 | 3 | 4 | 5 | …第二行 |
| 3 | 4 | 5 | 6 | …第三行 |
| 4 | 5 | 6 | 7 | …第四行 |
| 第一列 | 第二列 | 第三列 | 第四列 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f′(x)=6-3x2,g′(x)=ex | B. | f′(x)=-3x2,g′(x)=ex-1 | ||
| C. | f′(x)=-3x2,g′(x)=ex | D. | f′(x)=6-3x2,g′(x)=ex-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com