
【题目】已知正四棱柱ABCD﹣A1B1C1D1中,AB=2,AA1=4. 
(Ⅰ)求证:BD⊥A1C;
(Ⅱ)求二面角A﹣A1C﹣D1的余弦值;
(Ⅲ)在线段CC1上是否存在点P,使得平面A1CD1⊥平面PBD,若存在,求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)证明:∵ABCD﹣A1B1C1D1为正四棱柱,
∴AA1⊥平面ABCD,且ABCD为正方形.
∵BD平面ABCD,∴BD⊥AA1,BD⊥AC
∵AA1∩AC=A,∴BD⊥平面A1AC.
∵A1C平面A1AC,
∴BD⊥A1C.
(Ⅱ)解:如图,以D为原点建立空间直角坐标系D﹣xyz.
则D(0,0,0),A(2,0,0),C(0,2,0),A1(2,0,4),B1(2,2,4),
C1(0,2,4),D1(0,0,4),
∵ ![]() =(2,0,0),
=(2,0,0), ![]() =(0,2,﹣4).
=(0,2,﹣4).
设平面A1D1C的法向量 ![]() =(x1,y1,z1).
=(x1,y1,z1).
∴  .即
.即 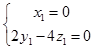 ,
,
令z1=1,则y1=2.∴ ![]() =(0,2,1).
=(0,2,1).
由(Ⅰ)知平面AA1C的法向量为 ![]() =(2,2,0)
=(2,2,0)
∴cos< ![]() >=
>= ![]() =
= ![]() .
.
∵二面角A﹣A1C﹣D1为钝二面角,
∴二面角A﹣A1C﹣D1的余弦值为﹣ ![]() .
.
(Ⅲ)解:设P(x2,y2,z2)为线段CC1上一点,且 ![]() =
= ![]() .
.
∵ ![]() =(x2,y2﹣2,z2),
=(x2,y2﹣2,z2), ![]() =(﹣x2,2﹣y2,4﹣z2).
=(﹣x2,2﹣y2,4﹣z2).
∴(x2,y2﹣2,z2)=λ(﹣x2,2﹣y2,4﹣z2).
即 ![]() .
.
∴P(0,2, ![]() ).
).
设平面PBD的法向量 ![]() .
.
∵ ![]() ,
, ![]() ,
,
∴  .即
.即 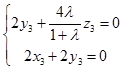 .
.
令y3=1,得 ![]() =(﹣1,1,﹣
=(﹣1,1,﹣ ![]() ).
).
若平面A1CD1⊥平面PBD,则 ![]() =0.
=0.
即2﹣ ![]() =0,解得
=0,解得 ![]() .
.
所以当 ![]() =
= ![]() 时,平面A1CD1⊥平面PBD
时,平面A1CD1⊥平面PBD
【解析】(Ⅰ)由已知条件推导出BD⊥AA1,BD⊥AC,从而得到BD⊥平面A1AC,由此能证明BD⊥A1C.(Ⅱ) 以D为原点建立空间直角坐标系D﹣xyz,利用向量法能求出二面角A﹣A1C﹣D1的余弦值.(Ⅲ)设P(x2,y2,z2)为线段CC1上一点,且 ![]() =
= ![]() ,利用向量法能求出当
,利用向量法能求出当 ![]() =
= ![]() 时,平面A1CD1⊥平面PBD.
时,平面A1CD1⊥平面PBD.
【考点精析】根据题目的已知条件,利用直线与平面平行的性质和直线与平面垂直的性质的相关知识可以得到问题的答案,需要掌握一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行;垂直于同一个平面的两条直线平行.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
=1的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
(Ⅰ)当t=4,|AM|=|AN|时,求△AMN的面积;
(Ⅱ)当2|AM|=|AN|时,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线y2=4x的焦点为F,过点F作直线l与抛物线分别交于两点A,B,若点M满足 ![]() =
= ![]() (
( ![]() +
+ ![]() ),过M作y轴的垂线与抛物线交于点P,若|PF|=2,则M点的横坐标为 .
),过M作y轴的垂线与抛物线交于点P,若|PF|=2,则M点的横坐标为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,
PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.
(Ⅰ)求证:平面EAC⊥平面PBC;
(Ⅱ)若二面角P﹣AC﹣E的余弦值为 ![]() ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)<f(x),且f(x+2)为偶函数,f(4)=1,则不等式f(x)<ex的解集为( )
A.(﹣2,+∞)
B.(0,+∞)
C.(1,+∞)
D.(4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走了378里路,第一天健步行走,从第二天起因脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”问此人第4天和第5天共走了( )
A.60里
B.48里
C.36里
D.24里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系xOy中,圆C的参数方程 ![]() (φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线l的极坐标方程是2ρsin(θ+ ![]() )=3
)=3 ![]() ,射线OM:θ=
,射线OM:θ= ![]() 与圆C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
与圆C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com