
【题目】设全集U=R,集合A={x|-1≤x<3},B={x|2x-4≥x-2}.
(1)求U(A∩B);
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
【答案】(1) U(A∩B)={x|x<2或x≥3}(2) a>-4.
【解析】试题分析:(1)求出集合B中不等式的解集确定出集合B,求出集合A与集合B的公共解集即为两集合的交集,根据全集为R,求出交集的补集即可;
(2)求出集合C中的不等式的解集,确定出集合C,由B与C的并集为集合C,得到集合B为集合C的子集,即集合B包含于集合C,从而列出关于a的不等式,求出不等式的解集即可得到a的范围.
解:(1)由集合B中的不等式2x﹣4≥x﹣2,解得x≥2,
∴B={x|x≥2},又A={x|﹣1≤x<3},
∴A∩B={x|2≤x<3},又全集U=R,
∴U(A∩B)={x|x<2或x≥3};
(2)由集合C中的不等式2x+a>0,解得x>﹣![]() ,
,
∴C={x|x>﹣![]() },
},
∵B∪C=C,
∴BC,
∴﹣![]() <2,解得a>﹣4;
<2,解得a>﹣4;
故a的取值范围为(﹣4,+∞).


科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
甲乙两个班级进行一门课程的考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如下的列联表:
班级与成绩列联表
优 秀 | 不优秀 | |
甲 班 | 10 | 35 |
乙 班 | 7 | 38 |
根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为成绩与班级有关系?
附:
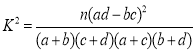
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|-1≤x<3},B={x|2x-4≥x-2}.
(1)求U(A∩B);
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类比平面内正三角形的“三边相等,三内角相等”的性质,可推出正四面体的下列一些性质,你认为比较恰当的是( )
①各棱长相等,同一顶点上的任两条棱的夹角都相等;②各个面都是全等的正三角形,相邻两个面所成的二面角都相等;③各个面都是全等的正三角形,同一顶点上的任两条棱的夹角都相等。
A. ① B. ②③ C. ①② D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在各项都不相等的等差数列{an}中,a1,a2是关于x的方程x2-7a4x+18a3=0的两个实根.
(1) 试判断-22是否在数列{an}中;
(2) 求数列{an}的前n项和Sn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,离心率为
,离心率为![]() .设过点
.设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同两点
相交于不同两点![]() ,
, ![]() 周长为
周长为![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知点![]() ,证明:当直线
,证明:当直线![]() 变化时,总有TA与
变化时,总有TA与![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com