
分析 逐项分析即可.①把函数的解析式变形可得;②双向判断是否成立即可判断正误;③根据复合命题的真值判断方法易得;④先求导数,由导数的几何意义即得.
解答 解:①∵$f(x)=1-2si{n}^{2}\frac{x}{2}=cosx$,∴T=2π,故①正确;
②当x=5时,有x2-4x-5=0,但当x2-4x-5=0时,不能推出x一定等于5,故“x=5”是“x2-4x-5=0”成立的充分不必要条件,故②错误;
③易知命题p为真,因为${x}^{2}-x+1=(x-\frac{1}{2})^{2}+\frac{3}{4}$>0,故命题q为真,所以p∧(¬q)为假命题,故③正确;
④∵f′(x)=3x2-6x,∴f′(1)=-3,∴在点(1,f(1))的切线方程为y-(-1)=-3(x-1),即3x+y-2=0,故④正确.
综上,正确的命题为①③④.
故答案为①③④.
点评 本题考查了充分必要条件、复合命题真假的判断以及导数的几何意义.考查对基本知识的掌握.属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | {1,2,6} | B. | {2,6} | C. | {6} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,3) | B. | (6,7] | C. | [6,7) | D. | [9,13) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
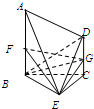 如图,已知AB⊥平面BEC,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形,F,G分别是AB,CD的中点.求证.
如图,已知AB⊥平面BEC,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形,F,G分别是AB,CD的中点.求证.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com