
【题目】在直角坐标平面内,已知![]() ,其中
,其中![]() 为正整数,对于平面上任意一点
为正整数,对于平面上任意一点![]() ,记
,记![]() 为
为![]() 关于
关于![]() 的对称点,
的对称点,![]() 为
为![]() 关于
关于![]() 的对称点,…
的对称点,…![]() 为
为![]() 关于
关于![]() 的对称点.
的对称点.
(1)求向量![]() 的坐标;
的坐标;
(2)对于任意偶数![]() ,用
,用![]() 表示向量
表示向量![]() 的坐标;
的坐标;
(3)当点![]() 在函数
在函数![]() 图像上移动时,点
图像上移动时,点![]() 形成的是函数
形成的是函数![]() 的图像,其中
的图像,其中![]() 是以3为周期的周期函数,且当
是以3为周期的周期函数,且当![]() 时,
时,![]() ,求:函数
,求:函数![]() 在
在![]() 上的解析式.
上的解析式.
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:高中数学 来源: 题型:
【题目】如图,马路![]() 南边有一小池塘,池塘岸
南边有一小池塘,池塘岸![]() 长40米,池塘的最远端
长40米,池塘的最远端![]() 到
到![]() 的距离为400米,且池塘的边界为抛物线型,现要在池塘的周边建一个等腰梯形的环池塘小路
的距离为400米,且池塘的边界为抛物线型,现要在池塘的周边建一个等腰梯形的环池塘小路![]() ,且
,且![]() 均与小池塘岸线相切,记
均与小池塘岸线相切,记![]() .
.

(1)求小路的总长,用![]() 表示;
表示;
(2)若在小路与小池塘之间(图中阴影区域)铺上草坪,求所需铺草坪面积最小时,![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的右顶点到其一条渐近线的距离等于
的右顶点到其一条渐近线的距离等于![]() ,抛物线
,抛物线![]() 的焦点与双曲线
的焦点与双曲线![]() 的右焦点重合,则抛物线
的右焦点重合,则抛物线![]() 上的动点
上的动点![]() 到直线
到直线![]() 和
和![]() 距离之和的最小值为( )
距离之和的最小值为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平行四边形![]() 中,
中,![]() 点
点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]()
(1)求证; 平面![]() 平面
平面![]() ;
;
(2)若平面![]() 和平面
和平面![]() 的交线为
的交线为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂用甲、乙两种不同工艺生产一大批同一种零件,零件尺寸均在[21.7,22.3](单位:cm)之间的零件,把零件尺寸在[21.9,22.1)的记为一等品,尺寸在[21.8,21.9)![]() [22.1,22.2)的记为二等品,尺寸在[21.7,21.8)
[22.1,22.2)的记为二等品,尺寸在[21.7,21.8)![]() [22.2,22.3]的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示:
[22.2,22.3]的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示:
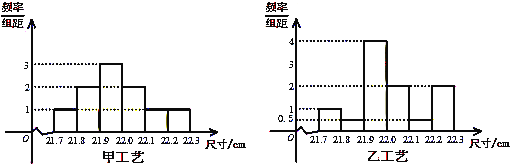
(Ⅰ)根据上述数据完成下列2×2列联表,根据此数据你认为选择不同的工艺与一等品产出率是否有关?
甲工艺 | 乙工艺 | 总计 | |
一等品 | |||
非一等品 | |||
总计 |
P(K2≥k) | 0.1 | 0.05 | 0.01 |
k | 2.706 | 3.841 | 6.635 |
附:![]() ,其中
,其中![]() .
.
(Ⅱ)以上述两种工艺中各种产品的频率作为相应产品产出的概率,若一等品、二等品、三等品的单件利润分别为30元、20元、15元,从一件产品的平均利润考虑,你认为以后该工厂应该选择哪种工艺生产该种零件?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (常数
(常数![]() ),P是曲线C上的动点,M是曲线C的右顶点,定点A的坐标为
),P是曲线C上的动点,M是曲线C的右顶点,定点A的坐标为![]() .
.
(1)若M与A重合,求曲线C的焦距.
(2)若![]() ,求
,求![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论:
①![]() ②
②![]() 是等边三角形 ③AB与平面BCD所成的角是
是等边三角形 ③AB与平面BCD所成的角是![]() ④AB与CD所成角为
④AB与CD所成角为![]() ,其中错误的结论个数是( )
,其中错误的结论个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意的![]() ,若数列
,若数列![]() 同时满足下列两个条件,则称数列
同时满足下列两个条件,则称数列![]() 具有“性质
具有“性质![]() ”.①
”.①![]() ;②存在实数
;②存在实数![]() 使得
使得![]() .
.
(1)数列![]() 中,
中,![]() ,判断
,判断![]() 是否具有“性质
是否具有“性质![]() ”.
”.
(2)若各项为正数的等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,证明:数列
,证明:数列![]() 具有“性质
具有“性质![]() ”,并指出
”,并指出![]() 的取值范围.
的取值范围.
(3)若数列![]() 的通项公式
的通项公式![]() ,对于任意的
,对于任意的![]() ,数列
,数列![]() 具有“性质
具有“性质![]() ”,且对满足条件的
”,且对满足条件的![]() 的最小值
的最小值![]() ,求整数
,求整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0),四点P1(1,1),P2(0,1),P3(–1,
(a>b>0),四点P1(1,1),P2(0,1),P3(–1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三点在椭圆C上.
)中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com