
【题目】在平面直角坐标系![]() 中,过定点
中,过定点![]() 作直线与抛物线
作直线与抛物线![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)已知![]() ,若点
,若点![]() 是点
是点![]() 关于坐标原点
关于坐标原点![]() 的对称点,求
的对称点,求![]() 面积的最小值;
面积的最小值;
(2)是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被以
被以![]() 为直径的圆截得的弦长恒为定值?若存在,求出
为直径的圆截得的弦长恒为定值?若存在,求出![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【答案】(1)![]() ;(2)满足条件的直线
;(2)满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ,详见解析.
,详见解析.
【解析】
(1)先得出点![]() 的坐标为
的坐标为![]() ,设
,设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 的方程与抛物线的方程联立,列出韦达定理,利用三角形的面积公式求出
的方程与抛物线的方程联立,列出韦达定理,利用三角形的面积公式求出![]() 的面积关于
的面积关于![]() 的表达式,由此可得出
的表达式,由此可得出![]() 面积的最小值;
面积的最小值;
(2)解法一:假设满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ,求出线段
,求出线段![]() 的中点
的中点![]() 的坐标,并计算出点
的坐标,并计算出点![]() 到直线
到直线![]() 的距离以及以
的距离以及以![]() 为直径的圆
为直径的圆![]() 的半径长,然后利用勾股定理可计算出
的半径长,然后利用勾股定理可计算出![]() 截以
截以![]() 为直径的圆所得弦长,结合弦长的表达式得出当
为直径的圆所得弦长,结合弦长的表达式得出当![]() 时,弦长为定值,从而得出直线
时,弦长为定值,从而得出直线![]() 的方程;
的方程;
解法二:假设满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ,求出以
,求出以![]() 为直径的圆的方程,将直线
为直径的圆的方程,将直线![]() 的方程与圆
的方程与圆![]() 的方程联立,列出韦达定理,利用弦长公式计算出
的方程联立,列出韦达定理,利用弦长公式计算出![]() 截以
截以![]() 为直径的圆所得弦长,结合弦长的表达式得出当
为直径的圆所得弦长,结合弦长的表达式得出当![]() 时,弦长为定值,从而得出直线
时,弦长为定值,从而得出直线![]() 的方程.
的方程.
(1)依题意,点![]() 的坐标为
的坐标为![]() ,
,
可设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
由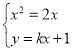 得
得![]() .
.
由韦达定理得![]() ,
,![]() .
.
于是![]() ,
,
![]() 当
当![]() 时,
时,![]() ;
;
(2)解法一:假设满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 与
与![]() 为直径的圆相交于点
为直径的圆相交于点![]() 、
、![]() ,
,![]() 的中点为
的中点为![]() ,则
,则![]() ,
,
![]() 点的坐标为
点的坐标为![]() ,
,![]() .
.
因为![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
令![]() ,得
,得![]() ,此时
,此时![]() 为定值,
为定值,
故满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ,即抛物线的通径所在的直线;
,即抛物线的通径所在的直线;
解法2:假设满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ,设以
,设以![]() 为直径的圆上任意一点为:
为直径的圆上任意一点为:![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
则以![]() 为直径的圆方程为:
为直径的圆方程为:![]() ,
,
化简为:![]() ,
,
直线方程![]() 代入上述方程得
代入上述方程得![]()
则![]()
设直线![]() 与以
与以![]() 为直径的圆的交点为
为直径的圆的交点为![]() ,
,![]() ,则有
,则有
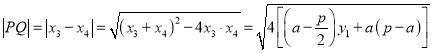
令![]() ,得
,得![]() ,此时
,此时![]() 为定值.
为定值.
故满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ,即抛物线的通径所在的直线.
,即抛物线的通径所在的直线.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元.为增加企业竞争力,决定优化产业结构,调整出![]() 名员工从事第三产业,调整后平均每人每年创造利润为
名员工从事第三产业,调整后平均每人每年创造利润为![]() 万元
万元![]() ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高![]() .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润条件下,若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则![]() 的取值范围是多少?
的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,然后纵坐标不变,横坐标变为原来的
个单位,然后纵坐标不变,横坐标变为原来的![]() 倍,得到
倍,得到![]() 的图象,下面四个结论正确的是( )
的图象,下面四个结论正确的是( )
A. 函数![]() 在区间
在区间![]() 上为增函数
上为增函数
B. 将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后得到的图象关于原点对称
个单位后得到的图象关于原点对称
C. 点![]() 是函数
是函数![]() 图象的一个对称中心
图象的一个对称中心
D. 函数![]() 在
在![]() 上的最大值为
上的最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况,在本市的所有中学生中随机抽取了120名学生进行调查,现将日均自学时间小于1小时的学生称为“自学不足”者![]() 根据调查结果统计后,得到如下
根据调查结果统计后,得到如下![]() 列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为
列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为![]() .
.
非自学不足 | 自学不足 | 合计 | |
配有智能手机 | 30 | ||
没有智能手机 | 10 | ||
合计 |
![]() 请完成上面的列联表;
请完成上面的列联表;
![]() 根据列联表的数据,能否有
根据列联表的数据,能否有![]() 的把握认为“自学不足”与“配有智能手机”有关?
的把握认为“自学不足”与“配有智能手机”有关?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为![]() (t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程![]() .
.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C交于A,B两点,![]() 为直线l上一点,求
为直线l上一点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线方程为y2=-4x,直线l的方程为2x+y-4=0,在抛物线上有一动点A,点A到y轴的距离为m,到直线l的距离为n,则m+n的最小值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】启东市政府拟在蝶湖建一个旅游观光项目,设计方案如下:如图所示的圆O是圆形湖的边界,沿线段AB,BC,CD,DA建一个观景长廊,其中A,B,C,D是观景长廊的四个出入口且都在圆O上,已知:BC=12百米,AB=8百米,在湖中P处和湖边D处各建一个观景亭,且它们关于直线AC对称,在湖面建一条观景桥APC.观景亭的大小、观景长廊、观景桥的宽度均忽略不计,设![]() .
.
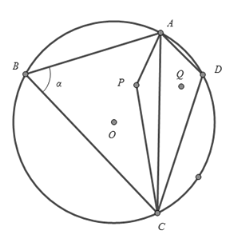
(1)若观景长廊AD=4百米,CD=AB,求由观景长廊所围成的四边形ABCD内的湖面面积;
(2)当![]() 时,求三角形区域ADC内的湖面面积的最大值;
时,求三角形区域ADC内的湖面面积的最大值;
(3)若CD=8百米且规划建亭点P在三角形ABC区域内(不包括边界),试判断四边形ABCP内湖面面积是否有最大值?若有,求出最大值,并写出此时![]() 的值;若没有,请说明理由.
的值;若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆C:
中,椭圆C:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,P为椭圆C上一点,且
,P为椭圆C上一点,且![]() 垂直于
垂直于![]() 轴,连结
轴,连结![]() 并延长交椭圆于另一点
并延长交椭圆于另一点![]() ,设
,设![]()
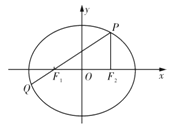
(1)若点![]() 的坐标为
的坐标为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)若![]() ,求椭圆
,求椭圆![]() 的离心率的取值范围
的离心率的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
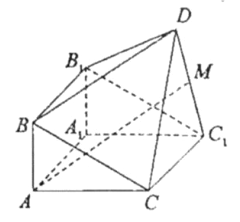
【题目】如图,由直三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中,![]() ,平面
,平面![]() 平面
平面![]()
(I)求证:![]() ;
;
(II)若M为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(III)在线段BC上(含端点)是否存在点P,使直线DP与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 得值,若不存在,说明理由.
得值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com