Question

3．如图所示，有一半径为R的半圆形钢板，计划剪裁成一等腰梯形ABCD的形状，它的下底AB是⊙O的直径，上底CD的端点在圆周上．
（1）写出这个梯形周长y与腰长x间的函数关系式，并求出它的定义域；
（2）求这个梯形周长的最大值及此时的腰长．

Answer 1

分析 （1）连接OD，OC，在△OAD中，若设∠AOD=θ，由余弦定理可得，cosθ=$\frac{2{R}^{2}-{x}^{2}}{2{R}^{2}}$；在△OCD中，由∠COD=180°-2θ，可得DC²=2R²-2R²•cos（180°-2θ），从而得DC；即得梯形的周长y和x的取值范围．
（2）利用配方法，可得这个梯形周长的最大值及此时的腰长．

解答 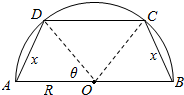解：（1）如图所示，连接OD，OC，则OC=OD=OA=OB=R，
在△OAD中，设∠AOD=θ，AD=x，由余弦定理，得
x²=2R²-2R²•cosθ，θ∈（0，90°），∴cosθ=$\frac{2{R}^{2}-{x}^{2}}{2{R}^{2}}$；
在△OCD中，∠COD=180°-2θ，同理：
DC²=2R²-2R²•cos（180°-2θ）=2R²（1+cos2θ）=2R²•2cos²θ=4R²•cos²θ，
∴DC=2R•cosθ=2R•$\frac{2{R}^{2}-{x}^{2}}{2{R}^{2}}$=2R-$\frac{{x}^{2}}{R}$；
所以梯形的周长：y=2R+2x+（2R-$\frac{{x}^{2}}{R}$）=-$\frac{{x}^{2}}{R}$+2x+4R；
∵x²=2R²-2R²•cosθ＜2R²，∴x＜$\sqrt{2}$R，∴定义域为（0，$\sqrt{2}$R）．
（2）y=-$\frac{{x}^{2}}{R}$+2x+4R=-$\frac{1}{R}$（x-R）²+5R，∴x=R，梯形周长的最大值5R．

点评 本题考查了余弦定理在解三角形中的应用，也考查了二倍角公式的灵活应用，考查配方法，属于中档题．