
已知数列 中,
中,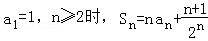
(1)求数列 的通项;
的通项;
(2)令 求数列
求数列 的前n项和Tn.
的前n项和Tn.
(1)an= ,(2)Tn=
,(2)Tn=

解析试题分析:(1)本题为由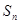 求
求 ,当
,当 时,
时, ,约去
,约去 整理得到关于
整理得到关于 的关系式
的关系式 所以
所以

 累加得
累加得 (2)因为
(2)因为 所以数列
所以数列 的前n项和为数列
的前n项和为数列 与数列
与数列 前n项和的和. 数列
前n项和的和. 数列 前n项和为
前n项和为 ,而数列
,而数列 前n项和需用错位相减法求解.运用错位相减法求和时需注意三点:一是相减时注意项的符号,二是求和时注意项的个数,三是最后结果需除以
前n项和需用错位相减法求解.运用错位相减法求和时需注意三点:一是相减时注意项的符号,二是求和时注意项的个数,三是最后结果需除以
试题解析:(1) ﹣
﹣ ,
,
移向整理得出
当n≥2时,an=(an﹣a n﹣1)+(a n﹣1﹣a n﹣2)+…+(a 2﹣a 1)+a1
= =1+
=1+ =
= ,n=1时也适合
,n=1时也适合
所以an= ,
,
(2)bn=nan= ,
,
Tn= ﹣(
﹣( )
)
令Tn′= ,两边同乘以
,两边同乘以 得
得 Tn′=
Tn′=
两式相减得出 Tn′=
Tn′=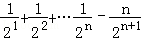 =
= =
=
Tn′=
所以Tn= ﹣(
﹣( )
)
=

考点:由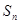 求
求 ,错位相减法求和
,错位相减法求和


科目:高中数学 来源: 题型:解答题
某地今年年初有居民住房面积为 m2,其中需要拆除的旧房面积占了一半,当地有关部门决定每年以当年年初住房面积的10%的住房增长率建设新住房,同时每年拆除xm2的旧住房,又知该地区人口年增长率为4.9‰.
m2,其中需要拆除的旧房面积占了一半,当地有关部门决定每年以当年年初住房面积的10%的住房增长率建设新住房,同时每年拆除xm2的旧住房,又知该地区人口年增长率为4.9‰.
(1)如果10年后该地区的人均住房面积正好比目前翻一番,那么每年应拆除的旧住房面积x是多少?
(2)依照(1)拆房速度,共需多少年能拆除所有需要拆除的旧房?
下列数据供计算时参考:
| 1.19=2.38 | 1.00499=1.04 |
| 1.110=2.6 | 1.004910=1.05 |
| 1.111=2.85 | 1.004911=1.06 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在数列{an}中,a1=2,an+1=4an-3n+1,n∈N*.
(1)求证:数列{an-n}是等比数列;
(2)求数列{an}的前n项和Sn;
(3)求证:不等式Sn+1≤4Sn对任意n∈N*皆成立.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知等比数列{an}满足:|a2-a3|=10,a1a2a3=125.
(1)求数列{an}的通项公式;
(2)是否存在正整数m,使得 ≥1?若存在,求m的最小值;若不存在,说明理由.
≥1?若存在,求m的最小值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com