
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() 是自然对数的底数),曲线
是自然对数的底数),曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直.
轴垂直.
(1)求![]() 的单调区间;
的单调区间;
(2)设![]() ,对任意
,对任意![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)根据导数的几何意义,曲线![]() 在
在![]() 处的切线方程的斜率就是
处的切线方程的斜率就是![]() ,写出方程即可求得
,写出方程即可求得![]() ,因此
,因此 ,设
,设![]() ,利用导数研究
,利用导数研究![]() 知当
知当![]() 时
时![]() ,从而
,从而![]() ,当
,当![]() 时
时![]() ,从而
,从而![]() ;(2)因为
;(2)因为![]() ,要证原式成立即证
,要证原式成立即证![]() 成立,先证明:对任意
成立,先证明:对任意![]() ,
,![]() 恒成立,再令
恒成立,再令![]() ,则
,则![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上递增,
上递增,![]() 恒成立,即
恒成立,即![]() ,即
,即![]() ,即
,即![]() ,而当
,而当![]() 时,有
时,有![]() ;当
;当![]() 时,由①②式,
时,由①②式,![]() ,故
,故![]() 时,
时,![]() 成立.
成立.
试题解析:(1)因为 ,由已知得
,由已知得![]() ,∴
,∴![]() .
.
所以 ,设
,设![]() ,则
,则![]() ,在
,在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上是减函数,由
上是减函数,由![]() 知,当
知,当![]() 时
时![]() ,从而
,从而![]() ,
,
当![]() 时
时![]() ,从而
,从而![]() .
.
综上可知,![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(2)因为![]() ,要证原式成立即证
,要证原式成立即证![]() 成立,
成立,
现证明:对任意![]() ,
,![]() 恒成立,当
恒成立,当![]() 时,由(1)知
时,由(1)知![]() 成立;
成立;
当![]() 时,
时,![]() ,且由(Ⅰ)知
,且由(Ⅰ)知![]() ,∴
,∴![]() .
.
设![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以当
,所以当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
所以![]() .即
.即![]() 时,
时,![]() .
.
综上所述,对任意![]() ,
,![]() 恒成立.①
恒成立.①
令![]() ,则
,则![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上递增,
上递增,
![]() 恒成立,即
恒成立,即![]() ,即
,即![]() .
.
②当![]() 时,有
时,有![]() ;当
;当![]() 时,由①②式,
时,由①②式,![]() ,
,
综上所述,![]() 时,
时,![]() 成立,故原不等式成立.
成立,故原不等式成立.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
【题目】某校高2010级数学培优学习小组有男生3人女生2人,这5人站成一排留影。
(1)求其中的甲乙两人必须相邻的站法有多少种?
(2)求其中的甲乙两人不相邻的站法有多少种?
(3)求甲不站最左端且乙不站最右端的站法有多少种 ?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴, 建立平面直角坐标系,在平面直角坐标系
轴的正半轴, 建立平面直角坐标系,在平面直角坐标系![]() 中, 直线
中, 直线![]() 经过点
经过点![]() ,倾斜角
,倾斜角![]() .
.
(1)写出曲线![]() 直角坐标方程和直线
直角坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点, 求
两点, 求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
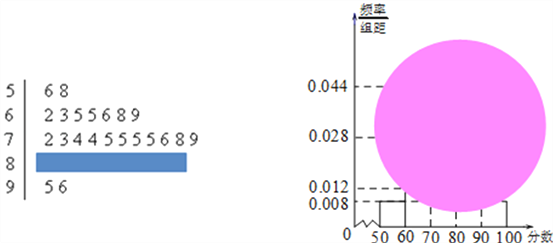
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(Ⅲ)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90,100)之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :坐标系与参数方程
:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,
,![]() 和
和![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了扩大该商品的影响力,提高年销售量,公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到![]() 元,公司拟投入
元,公司拟投入![]() 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入![]() 作为浮动宣传费用.试问:当该商品明年的销售量
作为浮动宣传费用.试问:当该商品明年的销售量![]() 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以坐标原点为极点,![]() 轴为正半轴建立极坐标系,圆
轴为正半轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为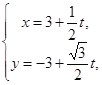 (t为参数).
(t为参数).
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)求直线![]() 分圆
分圆![]() 所得的两弧程度之比.
所得的两弧程度之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() ,若函数
,若函数![]() 的图象与x轴的任意两个相邻交点间的距离为
的图象与x轴的任意两个相邻交点间的距离为![]() ,当
,当![]() 时,函数
时,函数![]() 取得最大值
取得最大值![]() .
.
(1)求函数![]() 的解析式,并写出它的单调增区间;
的解析式,并写出它的单调增区间;
(2)若![]() ,求函数
,求函数![]() 的值域.
的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com