
分析 (1)通过2Sn=an+$\frac{1}{{a}_{n}}$计算出数列的前几项,进而猜想通项公式,利用数学归纳法证明即可;
(2)通过(1)分母有理化可知bn=(-1)n($\sqrt{n}$+$\sqrt{n-1}$),进而分n为奇数、偶数两种情况讨论即可.
解答 解:(1)∵Sn为an与$\frac{1}{{a}_{n}}$的等差中项,
∴2Sn=an+$\frac{1}{{a}_{n}}$,
当n=1时,易知a1=1,
当n=2时,2+2a2=a2+$\frac{1}{{a}_{2}}$,
整理得:${{a}_{2}}^{2}$+2a2-1=0,
解得:a2=$\sqrt{2}$-1或a2=-$\sqrt{2}$-1(舍),
当n=3时,2$\sqrt{2}$+2a3=a3+$\frac{1}{{a}_{3}}$,
整理得:${{a}_{3}}^{2}$+2$\sqrt{2}$a3-1=0,
解得:a3=$\sqrt{3}$-$\sqrt{2}$或a3=$\sqrt{3}$-$\sqrt{2}$(舍),
…
猜想:an=$\sqrt{n}$-$\sqrt{n-1}$.
下面用数学归纳法来证明:
①当n=1时,结论显然成立;
②假设当n=k-1(k≥2)时成立,即ak-1=$\sqrt{k-1}$-$\sqrt{k-2}$,
则2Sk=ak+$\frac{1}{{a}_{k}}$,即2$\sqrt{k-1}$+ak-$\frac{1}{{a}_{k}}$=0,
整理得:${{a}_{k}}^{2}$+2$\sqrt{k-1}$ak-1=0,
解得:ak=$\sqrt{k}$-$\sqrt{k-1}$或ak=-$\sqrt{k}$-$\sqrt{k-1}$(舍),
即当n=k时结论也成立;
由①②可知an=$\sqrt{n}$-$\sqrt{n-1}$.
(2)由(1)可知bn=$\frac{{(-1)}^{n}}{{a}_{n}}$=$\frac{(-1)^{n}}{\sqrt{n}-\sqrt{n-1}}$=(-1)n($\sqrt{n}$+$\sqrt{n-1}$),
当n为奇数时,Tn=-1+($\sqrt{2}$+1)-($\sqrt{3}$+$\sqrt{2}$)+…+($\sqrt{n-1}$+$\sqrt{n-2}$)-($\sqrt{n}$+$\sqrt{n-1}$)
=-$\sqrt{n}$,
当n为偶数时,Tn=-1+($\sqrt{2}$+1)-($\sqrt{3}$+$\sqrt{2}$)+…-($\sqrt{n-1}$+$\sqrt{n-2}$)+($\sqrt{n}$+$\sqrt{n-1}$)
=$\sqrt{n}$,
综上所述,Tn=$\left\{\begin{array}{l}{-\sqrt{n},n为奇数}\\{\sqrt{n},n为偶数}\end{array}\right.$.
点评 本题考查数列的通项及前n项和,考查数学归纳法,考查分类讨论的思想,注意解题方法的积累,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
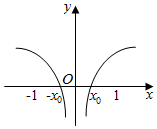
| A. | $\frac{{e}^{x}}{x}$ | B. | x2•lnx | C. | $\frac{{e}^{|x|}}{x}$ | D. | x•lnx2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin1•f($\frac{1}{2}$)>sin$\frac{1}{2}$•f(1) | B. | $\frac{1}{2}$•f($\frac{1}{2}$)>sin$\frac{1}{2}$•f($\frac{π}{6}$) | ||
| C. | sin2•f(1)>sin1•f(2) | D. | f($\frac{π}{3}$)>$\sqrt{3}$f($\frac{π}{6}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com