
【题目】如图,在三棱台ABC﹣DEF中,已知平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3,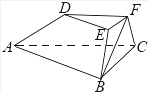
(1)求证:EF⊥平面ACFD;
(2)求二面角B﹣AD﹣F的余弦值.
【答案】
(1)
证明:延长AD,BE,CF相交于点K,如图所示,
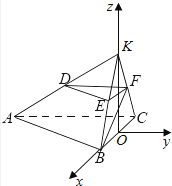
∵平面BCFE⊥平面ABC,∠ACB=90°,
∴AC⊥平面BCK,∴BF⊥AC.
又EF∥BC,BE=EF=FC=1,BC=2,∴△BCK为等边三角形,且F为CK的中点,则BF⊥CK,
∴BF⊥平面ACFD
(2)
方法一:过点F作FQ⊥AK,连接BQ,∵BF⊥平面ACFD.∴BF⊥AK,则AK⊥平面BQF,
∴BQ⊥AK.∴∠BQF是二面角B﹣AD﹣F的平面角.
在Rt△ACK中,AC=3,CK=2,可得FQ= ![]() .
.
在Rt△BQF中,BF= ![]() ,FQ=
,FQ= ![]() .可得:cos∠BQF=
.可得:cos∠BQF= ![]() .
.
∴二面角B﹣AD﹣F的平面角的余弦值为 ![]() .
.
方法二:如图
 ,
,
延长AD,BE,CF相交于点K,则△BCK为等边三角形,
取BC的中点,则KO⊥BC,又平面BCFE⊥平面ABC,∴KO⊥平面BAC,
以点O为原点,分别以OB,OK的方向为x,z的正方向,建立空间直角坐标系O﹣xyz.
可得:B(1,0,0),C(﹣1,0,0),K(0,0, ![]() ),A(﹣1,﹣3,0),
),A(﹣1,﹣3,0), ![]() ,
, ![]() .
.
![]() =(0,3,0),
=(0,3,0), ![]() =
= ![]() ,
, ![]() (2,3,0).
(2,3,0).
设平面ACK的法向量为 ![]() =(x1,y1,z1),平面ABK的法向量为
=(x1,y1,z1),平面ABK的法向量为 ![]() =(x2,y2,z2),由
=(x2,y2,z2),由 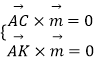 ,可得
,可得 ![]() ,
,
取 ![]() =
= ![]() .
.
由 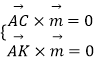 ,可得
,可得 ![]() ,取
,取 ![]() =
= ![]() .
.
∴ ![]() =
= ![]() =
= ![]() .
.
∴二面角B﹣AD﹣F的余弦值为 ![]() .
.
【解析】(1)先证明BF⊥AC,再证明BF⊥CK,进而得到BF⊥平面ACFD.
(2)方法一:先找二面角B﹣AD﹣F的平面角,再在Rt△BQF中计算,即可得出;
方法二:通过建立空间直角坐标系,分别计算平面ACK与平面ABK的法向量,进而可得二面角B﹣AD﹣F的平面角的余弦值.
本题考查了空间位置关系、法向量的应用、空间角,考查了空间想象能力、推理能力与计算能力,属于中档题.
【考点精析】利用空间中直线与直线之间的位置关系对题目进行判断即可得到答案,需要熟知相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设F1 , F2分别是C: ![]() (a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N. 
(1)若直线MN的斜率为 ![]() ,求C的离心率;
,求C的离心率;
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() +y2=1(m>1)与双曲线C2:
+y2=1(m>1)与双曲线C2: ![]() ﹣y2=1(n>0)的焦点重合,e1 , e2分别为C1 , C2的离心率,则( )
﹣y2=1(n>0)的焦点重合,e1 , e2分别为C1 , C2的离心率,则( )
A.m>n且e1e2>1
B.m>n且e1e2<1
C.m<n且e1e2>1
D.m<n且e1e2<1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg![]() 的图象关于原点对称,其中a为常数.
的图象关于原点对称,其中a为常数.
(Ⅰ)求a的值,并求出f(x)的定义域
(Ⅱ)关于x的方程f(2x)+21g(2x-1)=a在x∈[![]() ,
,![]() ]有实数解,求a的取值范围.
]有实数解,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4sinxcos(x+![]() )+1.
)+1.
(1)求f(![]() )的值;
)的值;
(2)求f(x)的最小正周期;
(3)求f(x)在区间[0,![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+bx+c,若对任意的x1,x2∈[-1,1],有|f(x1)-f(x2)|≤6,则b的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com