
���� ��1����������Ϊ�������У���ϵ���ʽ�ɵ�an+1-an=2��b2=-2b1��bn+2=2bn+1��n��N*���ɴ˿ɵ�����{an}Ϊ�Ȳ����У�����{bn}�ӵڶ����ɵȱ����У�Ȼ�����õȲ����к͵ȱ����е�ͨ�ʽ��ô𰸣�
��2���ٸ�����Ŀ�����жϣ�����{an}��Ϊ1��3��5��7��5��7��9��11��������ǰ4��Ϊ����Ϊ1������Ϊ2�ĵȲ����У��ӵ�5�ʼΪ����5������Ϊ2�ĵȲ����У����Sn���ɣ�
����������{bn}Ϊ�������С���b1=-1���ۺ��ж�����{bn}������ֻ����������������������m��ʹ��Sm+1=Tm����Ȼm��1����TmΪ��������{an}�и����Ϊ�������ɵ�m��Ϊż���� �����ò���ʽ֤��m��6��������м��ɣ�
��� �⣺��1��������{an}��{bn}��Ϊ�������У�
���ɵ���ʽ�ɵ�an+1-an=2��b2=-2b1��bn+2=2bn+1��n��N*��
������{an}Ϊ�Ȳ����У�����{bn}�ӵڶ����ɵȱ����У�
��an=2n-1��${b}_{n}=\left\{\begin{array}{l}{-1��n=1}\\{{2}^{n-1}��n��2}\end{array}\right.$��
��2���١�����{an}���㣺����Ψһ��������k=5��ʹ��ak��ak-1����|an+1-an|=2��
������{an}��Ϊ1��3��5��7��5��7��9��11��������ǰ4��Ϊ����Ϊ1������Ϊ2�ĵȲ����У��ӵ�5�ʼΪ����5������Ϊ2�ĵȲ����У�
��${S}_{n}=\left\{\begin{array}{l}{{n}^{2}��n��4}\\{{n}^{2}-4n+16��n��5}\end{array}\right.$��
�ڡ�$|\frac{{b}_{n+1}}{{b}_{n}}|=2$����bn+1=��2bn��
��|bn|=2n-1��
������{bn}Ϊ�������С���b1=-1��
������{bn}������ֻ���������
�������������m��ʹ��Sm+1=Tm����Ȼm��1����TmΪ��������{an}�и����Ϊ������
��m��Ϊż����
����֤����m��6��
��m��7������{an}��Sm+1��max=1+3+��+��2m+1��=��m+1��2��
������{bn}�У�bm��ȻΪ��������${T}_{m}=-1+{b}_{2}+��+��-{2}^{m-1}��$��-1+21+��+2m-2+��-2m-1��=-3��0����Ȼì�ܣ�
��$��{T}_{m}��_{min}=-1+{2}^{1}+��+{2}^{m-3}+��-{2}^{m-2}��+{2}^{m-1}$=2m-1-3��
��${c}_{m}={2}^{m-1}-��m+1��^{2}-3$��
��${d}_{m}={c}_{m+1}-{c}_{m}={2}^{m-1}-2m-3$��
��${d}_{m+1}-{d}_{m}={2}^{m-1}-2��$0��m��7����
��{dm}��m��7��Ϊ�����У���d7��0����{cm}��m��7��Ϊ�����У���c8��0��
�ࣨTm��min����Sm��max��
��m��6��
��m=6ʱ�����죺{an}Ϊ1��3��1��3��5��7��9������{bn}Ϊ-1��2��4��8��-16��32��64����
��ʱp=2��q=4��
��mmax=6����Ӧ��p=2��q=4��
���� �������¶����⣬���������е���ʽ���ۺϿ���ѧ�������¶���������е����⣬�����˷�������ͽ��������������������⣮


 �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | tan735�㣾tan800�� | B�� | tan1��-tan2 | C�� | tan$\frac{5��}{7}$��tan$\frac{4��}{7}$ | D�� | tan$\frac{9��}{8}$��tan$\frac{��}{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 45�� | B�� | -50�� | C�� | -40�� | D�� | 920�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0⊆A | B�� | {0}��A | C�� | ∅��A | D�� | {0}⊆A |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������������и��������ܿ�����ѧ�������Ծ��������棩 ���ͣ�ѡ����
һ���ڴ�װ��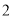 �������
�������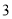 ���������������������Żأ�������������ĸ����ǣ� ��
���������������������Żأ�������������ĸ����ǣ� ��
A��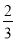 B��
B��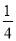 C��
C��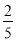 D��
D��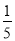
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com