
| A. | tan735°>tan800° | B. | tan1>-tan2 | C. | tan$\frac{5π}{7}$<tan$\frac{4π}{7}$ | D. | tan$\frac{9π}{8}$<tan$\frac{π}{7}$ |
分析 利用诱导公式化简三角函数,利用函数的单调性判断大小关系即可.
解答 解:720°<735°<720°+80°,可得tan735°<tan800°;
-tan2=tan(π-2),而1$<π-2<\frac{π}{2}$,所以tan1<-tan2;
π>$\frac{5π}{7}$>$\frac{4π}{7}$$>\frac{π}{2}$,tan$\frac{5π}{7}$>tan$\frac{4π}{7}$,
tan$\frac{9π}{8}$=tan$\frac{π}{8}$<tan$\frac{π}{7}$;
故选:D.
点评 本题考查三角函数线以及诱导公式的应用,考查计算能力.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:解答题
 已知扇形AOB的圆心角∠AOB=$\frac{π}{6}$,半径OA=1,在$\widehat{AB}$上有一个动点M,过M作矩形MNPQ,如图,设∠AOM=θ,记矩形MNPQ的面积为S.
已知扇形AOB的圆心角∠AOB=$\frac{π}{6}$,半径OA=1,在$\widehat{AB}$上有一个动点M,过M作矩形MNPQ,如图,设∠AOM=θ,记矩形MNPQ的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1≥-5 | B. | a1≥-1 | C. | a1≥-1或a1≤-5 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
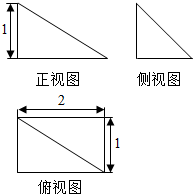
| A. | $\frac{7+2\sqrt{2}+\sqrt{5}}{2}$ | B. | $\frac{3+2\sqrt{2}+\sqrt{6}}{2}$ | C. | $\frac{7+2\sqrt{2}+6}{2}$ | D. | $\frac{3+2\sqrt{2}+\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com