Question

【题目】已知二次函数f(x)＝ax2＋bx＋c(a，b，c∈R)满足：对任意实数x，都有f(x)≥x，且当x∈(1,3)时，有f(x)≤ (x＋2)2成立．

(1)证明：f(2)＝2；

(2)若f(－2)＝0，求f(x)的表达式；

(3)设g(x)＝f(x)－x，x∈[0，＋∞)，若g(x)图象上的点都位于直线y＝的上方，求实数m的取值范围．

Answer 1

【答案】（1）见解析（2）f(x)＝x2＋x＋.（3）m∈(－∞，1＋)．

【解析】

（1）由题得，所以f(2)=2.（2）由f(2)=2，f(－2)＝0得到a,b,c的方程组，再根据f(x)≥x恒成立得到ax2＋(b－1)x＋c≥0恒成立，即a>0.Δ＝(－1)2－4a(1－4a)≤0，解出a,b,c的值即得f(x)的表达式.(3)先转化为x2＋4(1－m)x＋2>0在x∈[0，＋∞)恒成立，再利用二次函数的图像数形结合分析得到m的取值范围.

(1)证明：由条件知：

f(2)＝4a＋2b＋c≥2恒成立．

又因取x＝2时，f(2)＝4a＋2b＋c≤ (2＋2)2＝2恒成立，∴f(2)＝2.

(2)因，

∴4a＋c＝2b＝1.

∴b＝，c＝1－4a.　

又f(x)≥x恒成立，即ax2＋(b－1)x＋c≥0恒成立．

∴a>0.Δ＝(－1)2－4a(1－4a)≤0，

解出：a＝，b＝，c＝.

∴f(x)＝x2＋x＋.

(3)g(x)＝x2＋(－)x＋>在x∈[0，＋∞)必须恒成立．

即x2＋4(1－m)x＋2>0在x∈[0，＋∞)恒成立，

①Δ<0，即[4(1－m)]2－8<0.

解得：1－<m<1＋.

②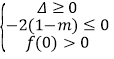解得：m≤1－，

综上m∈(－∞，1＋)．