
分析 (1)由an=2an-1+2n-1(n≥2,n∈N*)可得:$\frac{{a}_{n}-1}{{2}^{n}}$-$\frac{{a}_{n-1}-1}{{2}^{n-1}}$=1(n≥2,n∈N*),利用等差数列的定义可证数列{$\frac{{{a_n}-1}}{2^n}$}为等差数列,再求得其首项$\frac{{a}_{1}-1}{{2}^{1}}$=2,即可求得数列{an}的通项公式;
(2)由an=(n+1)•2n+1,bn=lg$\frac{{{a_n}-1}}{n}$,可求得bn=lg(n+1)-lgn+nlg2,利用分组求和法可求得数列{bn}的前n项和Sn.
解答 (1)证明:∵a1=5,an=2an-1+2n-1(n≥2,n∈N*),
an-1=2(an-1-1)+2n(n≥2,n∈N*),
∴$\frac{{a}_{n}-1}{{2}^{n}}$=$\frac{{a}_{n-1}-1}{{2}^{n-1}}$+1,即$\frac{{a}_{n}-1}{{2}^{n}}$-$\frac{{a}_{n-1}-1}{{2}^{n-1}}$=1,
∴数列{$\frac{{{a_n}-1}}{2^n}$}是公差为1的等差数列,又a1=5,$\frac{{a}_{1}-1}{{2}^{1}}$=2,
∴$\frac{{a}_{n}-1}{{2}^{n}}$=2+(n-1)×1=n+1,
∴an=(n+1)•2n+1.
(2)解:∵bn=lg$\frac{{{a_n}-1}}{n}$=lg$\frac{(n+1{)•2}^{n}}{n}$=lg(n+1)-lgn+nlg2,
∴Sn=b1+b2+…+bn
=[(lg2-lg1)+(lg3-lg2)+…+(lg(n+1)-lgn)]+lg2•(1+2+3+…+n)
=[lg(n+1)-lg1]+$\frac{n(n+1)}{2}$lg2
=lg(n+1)+$\frac{n(n+1)}{2}$lg2.
点评 本题考查数列的求和,考查等差关系的确定及其通项的求法,突出考查等价转化思想与分组求和法的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{n}{n+1}$ | B. | $\frac{4n}{n+1}$ | C. | $\frac{3n}{n+1}$ | D. | $\frac{5n}{n+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知△OCB中,A是BC边的中点,D是OB边上靠近点B的三等分点,DC与OA相交于点E,DE:DC=2:5,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$
如图,已知△OCB中,A是BC边的中点,D是OB边上靠近点B的三等分点,DC与OA相交于点E,DE:DC=2:5,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
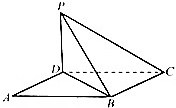 如图,在平行四边形ABCD中,BD=4$\sqrt{3}$,PD⊥平面ABCD,平面PBC⊥平面PBD,二面角P-BC-D为60°
如图,在平行四边形ABCD中,BD=4$\sqrt{3}$,PD⊥平面ABCD,平面PBC⊥平面PBD,二面角P-BC-D为60°查看答案和解析>>
科目:高中数学 来源: 题型:填空题
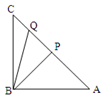 如图,在等腰直角△ABC,∠ABC=90°,AB=2$\sqrt{2}$,点P在线段AC上,若点Q在线段PC上,且∠PBQ=30°,则△BPQ的面积的最小值为8-4$\sqrt{3}$.
如图,在等腰直角△ABC,∠ABC=90°,AB=2$\sqrt{2}$,点P在线段AC上,若点Q在线段PC上,且∠PBQ=30°,则△BPQ的面积的最小值为8-4$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com