
| 13 |
| 3 |
| AO |
| BC |
| 3 |
 解:(1)由(sinA+sinB+sinC)(sinB+sinC-sinA)=3sinBsinC,
解:(1)由(sinA+sinB+sinC)(sinB+sinC-sinA)=3sinBsinC,| b2+c2-a2 |
| 2bc |
| bc |
| 2bc |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| 3 |
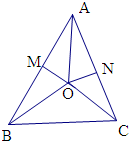
| AO |
| BC |
| AO |
| AC |
| AB |
| AO |
| AC |
| AO |
| AB |
| AM |
| AC |
| AN |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
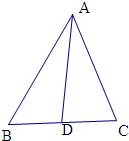 由余弦定理可得a2=b2+c2-2bccos60°,
由余弦定理可得a2=b2+c2-2bccos60°,| 1 |
| 2 |
| 3+AD2-c2 | ||
2
|
| 3+AD2-b2 | ||
2
|
| 3 |


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
| 学生 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
| 甲 | 56 | 57 | 69 | 76 | 91 | 92 |
| 乙 | 66 | 81 | 70 | 88 | 86 | 93 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com