
| A. | (7+4$\sqrt{3}$,+∞) | B. | (7-4$\sqrt{3}$,+∞) | C. | (7-4$\sqrt{3}$,7+4$\sqrt{3}$) | D. | (0,7-4$\sqrt{3}$)∪(7+4$\sqrt{3}$,+∞) |
分析 根据双曲线渐近线的方程求出交点P的坐标,结合点与圆的关系建立不等式关系进行求解即可.
解答 解:过F1(-c,0)且与渐近线y=bx平行的直线为y=b(x+c),
与另外一条渐近线y=-bx联立得$\left\{\begin{array}{l}{y=b(x+c)}\\{y=-bx}\end{array}\right.$,得$\left\{\begin{array}{l}{x=-\frac{c}{2}}\\{y=\frac{bc}{2}}\end{array}\right.$,即P(-$\frac{c}{2}$,$\frac{bc}{2}$),
以原点为圆心,双曲线M的虚轴长为半径的圆的方程为x2+y2=4b2,
∴(-$\frac{c}{2}$)2+($\frac{bc}{2}$)2<4b2,即c2+b2c2<16b2,
把c2=b2+1代入并整理得b4-14b2+1<0,
得7-4$\sqrt{3}$<b2<7+4$\sqrt{3}$,
即b2的取值范围是(7-4$\sqrt{3}$,7+4$\sqrt{3}$),
故选:C
点评 本题主要考查双曲线的方程和性质,根据渐近线方程求出交点坐标,结合点与圆的位置关系建立不等式关系是解决本题的关键.


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{1}=1$ | D. | ${x^2}-\frac{y^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
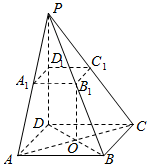 在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.
在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\frac{9\sqrt{3}}{4}$ | D. | $\frac{27\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com