
【题目】已知函数![]() .
.
(1)当![]() 时,判断函数
时,判断函数![]() 的单调性;
的单调性;
(2)若函数![]() 在
在![]() 处取得极小值,求实数a的取值范围.
处取得极小值,求实数a的取值范围.
【答案】(1)函数![]() 在区间
在区间![]() 单调递减(2)
单调递减(2)![]()
【解析】
(1)当![]() 时,求得函数的导数
时,求得函数的导数![]() ,构造函数
,构造函数![]() ,利用导数求得
,利用导数求得![]() 的单调性与最值,进而得出
的单调性与最值,进而得出![]() 的符号,即可求解函数
的符号,即可求解函数![]() 的单调性;
的单调性;
(2)求得函数![]() 导数
导数![]() ,构造新函数
,构造新函数![]() ,求得
,求得![]() 的导数,分
的导数,分![]() ,
,![]() ,
,![]() ,
,![]() 四种情况讨论,求得
四种情况讨论,求得![]() 的单调性与最值,得出
的单调性与最值,得出![]() 单调性,即可求解
单调性,即可求解![]() 的极值,进而得到
的极值,进而得到![]() 的范围.
的范围.
(1)当![]() 时,
时,![]() ,定义域为
,定义域为![]() ,
,
![]() ,设
,设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
所以函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
![]() 的最大值为
的最大值为![]() ,所以当
,所以当![]() 时,
时,![]() ,即
,即![]()
所以函数![]() 在区间
在区间![]() 单调递减
单调递减
(2)由已知得:![]() ,则
,则![]() ,
,
记![]() ,则
,则![]() ,
,![]() ,
,
①若![]() 时,则当
时,则当![]() 时
时![]() ,
,![]() 在
在![]() 单调递增
单调递增
且当![]() 时,
时,![]() ,即
,即![]()
当![]() 时,
时,![]() ,即
,即![]()
又![]() ,所以函数
,所以函数![]() 在
在![]() 处取得极小值,满足题意.
处取得极小值,满足题意.
②若![]() 时,则
时,则![]() ,当
,当![]() 时,
时,![]() ,故函数
,故函数![]() 区间
区间![]() 单调递增,
单调递增,
且当![]() 时
时![]() 即
即![]()
当![]() 时
时![]() ,即
,即![]()
又![]() ,所以函数
,所以函数![]() 在
在![]() 处取得极小值,满足题意.
处取得极小值,满足题意.
③若![]() 时,则
时,则![]() ,由(1)知函数
,由(1)知函数![]() 在区间
在区间![]() 单调递减,
单调递减,
故![]() 在区间
在区间![]() 单调递减,不满足题意.
单调递减,不满足题意.
④若![]() 时,则
时,则![]() ,当
,当![]() 时
时![]() ,故函数
,故函数![]() 在
在![]() 单调递减
单调递减
且当![]() 时,
时,![]() ,即
,即![]()
当![]() 时,
时,![]() ,即
,即![]() ,又
,又![]() ,
,
所以函数![]() 在
在![]() 处取得极大值,不满足题意.
处取得极大值,不满足题意.
综上,实数a的取值范围是![]()


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点..
的中点..
(1)求证:平面![]() 平面
平面![]() ;
;
(2)![]() ,在线段
,在线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() .请说明理由.
.请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin ωx·cos ωx+![]() cos2ωx-
cos2ωx-![]()
(ω>0),直线x=x1,x=x2是y=f(x)图象的任意两条对称轴,且|x1-x2|的最小值为![]() .
.
(Ⅰ)求f(x)的表达式;
(Ⅱ)将函数f(x)的图象向右平移![]() 个单位长度后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的单调减区间.
个单位长度后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的单调减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 存在两个极值点
存在两个极值点![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若不等式![]() 对任意的实数
对任意的实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过
,过![]() 的直线交
的直线交![]() 轴正半轴于点
轴正半轴于点![]() ,交抛物线于
,交抛物线于![]() 两点,其中点
两点,其中点![]() 在第一象限.
在第一象限.
(Ⅰ)求证:以线段![]() 为直径的圆与
为直径的圆与![]() 轴相切;
轴相切;
(Ⅱ)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表为![]() 年至
年至![]() 年某百货零售企业的线下销售额(单位:万元),其中年份代码
年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 |
|
|
|
|
线下销售额 |
|
|
|
|
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 年该百货零售企业的线下销售额;
年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了![]() 位男顾客、
位男顾客、![]() 位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有
位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有![]() 人、女顾客有
人、女顾客有![]() 人,能否在犯错误的概率不超过
人,能否在犯错误的概率不超过![]() 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据: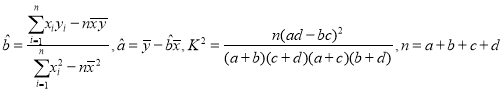 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设抛物线![]() 的准线
的准线![]() 与
与![]() 轴交于椭圆
轴交于椭圆![]() 的右焦点
的右焦点![]() ,
,![]() 为左焦点,椭圆的离心率为
为左焦点,椭圆的离心率为![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 交于
交于![]() 轴上方一点
轴上方一点![]() ,连接
,连接![]() 并延长
并延长![]() 交
交![]() 于点
于点![]() 为
为![]() 上一动点,且在
上一动点,且在![]() 之间移动.
之间移动.
(1)当![]() 取最小值时,求
取最小值时,求![]() 和
和![]() 的方程;
的方程;
(2)若![]() 的边长恰好是三个连接的自然数,求
的边长恰好是三个连接的自然数,求![]() 面积的最大值.
面积的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大提出,坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村真脱贫,坚持扶贫同扶智相结合,帮助贫困村种植蜜柚,并利用电商进行销售,为了更好地销售,现从该村的蜜柚树上随机摘下了100个蜜柚进行测重,其质量分别在![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (单位:克)中,其频率分布直方图如图所示.
(单位:克)中,其频率分布直方图如图所示.

(1)按分层抽样的方法从质量落在![]() ,
, ![]() 的蜜柚中抽取5个,再从这5个蜜柚中随机抽取2个,求这2个蜜柚质量均小于2000克的概率;
的蜜柚中抽取5个,再从这5个蜜柚中随机抽取2个,求这2个蜜柚质量均小于2000克的概率;
(2)以各组数据的中间数代表这组数据的平均水平,以频率代表概率,已知该贫困村的蜜柚树上大约还有5000个蜜柚等待出售,某电商提出两种收购方案:
A.所有蜜柚均以40元/千克收购;
B.低于2250克的蜜柚以60元/个收购,高于或等于2250克的以80元/个收购.
请你通过计算为该村选择收益最好的方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在区间D上的函数![]() ,若存在闭区间
,若存在闭区间![]() 和常数
和常数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,且对任意
,且对任意![]() ∈D,当
∈D,当![]() 时,
时,![]() 恒成立,则称函数
恒成立,则称函数![]() 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.
(Ⅰ)判断函数![]() 和
和![]() 是否为R上的“平底型”函数? 并说明理由;
是否为R上的“平底型”函数? 并说明理由;
(Ⅱ)设![]() 是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式
是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式![]() 对一切
对一切![]() R恒成立,求实数
R恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若函数![]() 是区间
是区间![]() 上的“平底型”函数,求
上的“平底型”函数,求![]() 和
和![]() 的值.
的值.
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com