
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过
,过![]() 的直线交
的直线交![]() 轴正半轴于点
轴正半轴于点![]() ,交抛物线于
,交抛物线于![]() 两点,其中点
两点,其中点![]() 在第一象限.
在第一象限.
(Ⅰ)求证:以线段![]() 为直径的圆与
为直径的圆与![]() 轴相切;
轴相切;
(Ⅱ)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】 如图,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的中点,沿
的中点,沿![]() 将
将![]() 折起,得到如图所示的四棱锥
折起,得到如图所示的四棱锥![]()

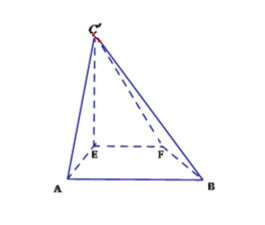
(1)求证:![]() 平面
平面![]() ;
;
(2)当四棱锥![]() 体积取最大值时,
体积取最大值时,
(i) 写出最大体积;
(ii) 求![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个说法:
①已知向量![]() ,
, ![]() ,若
,若![]() 与
与![]() 的夹角为钝角,则
的夹角为钝角,则![]() ;
;
②先将函数![]() 的图象上各点纵坐标不变,横坐标缩小为原来的
的图象上各点纵坐标不变,横坐标缩小为原来的![]() 后,再将所得函数图象整体向左平移
后,再将所得函数图象整体向左平移![]() 个单位,可得函数
个单位,可得函数![]() 的图象;
的图象;
③函数![]() 有三个零点;
有三个零点;
④函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
其中正确的是__________.(填上所有正确说法的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某机械厂欲从![]() 米,
米,![]() 米的矩形铁皮中裁剪出一个四边形
米的矩形铁皮中裁剪出一个四边形![]() 加工成某仪器的零件,裁剪要求如下:点
加工成某仪器的零件,裁剪要求如下:点![]() 分别在边
分别在边![]() 上,且
上,且![]() ,
,![]() .设
.设![]() ,四边形
,四边形![]() 的面积为
的面积为![]() (单位:平方米).
(单位:平方米).

(1)求![]() 关于
关于![]() 的函数关系式,求出定义域;
的函数关系式,求出定义域;
(2)当![]() 的长为何值时,裁剪出的四边形
的长为何值时,裁剪出的四边形![]() 的面积最小,并求出最小值.
的面积最小,并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙二人去看望高中数学张老师,期间他们做了一个游戏,张老师的生日是![]() 月
月![]() 日,张老师把
日,张老师把![]() 告诉了甲,把
告诉了甲,把![]() 告诉了乙,然后张老师列出来如下10个日期供选择: 2月5日,2月7日,2月9日,3月2日,3月7日,5月5日,5月8日,7月2日,7月6日,7月9日.看完日期后,甲说“我不知道,但你一定也不知道”,乙听了甲的话后,说“本来我不知道,但现在我知道了”,甲接着说,“哦,现在我也知道了”.请问张老师的生日是_______.
告诉了乙,然后张老师列出来如下10个日期供选择: 2月5日,2月7日,2月9日,3月2日,3月7日,5月5日,5月8日,7月2日,7月6日,7月9日.看完日期后,甲说“我不知道,但你一定也不知道”,乙听了甲的话后,说“本来我不知道,但现在我知道了”,甲接着说,“哦,现在我也知道了”.请问张老师的生日是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解重庆市高中学生在面对新高考模式“3+1+2”的科目选择中,物理与历史的二选一是否与性别有关,某高中随机对该校50名高一学生进行了问卷调查得到相关数据如下列联表:
选物理 | 选历史 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 |
己知在这50人中随机抽取1人,抽到选物理的人的概率为![]() 。
。
(1)请将上面的列联表补充完整,并判断是否有99.5%的把握认为物理与历史的二选一与性别有关?
| 0.15 | 0.10 | 0.05 | 0.01 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(参考公式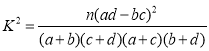 ,其中
,其中![]() 为样本容量)
为样本容量)
(2)己知在选物理的10位女生中有3人选择了化学、地理,有5人选择了化学、生物,有2人选择了生物、地理,现从这10人中抽取3人进行更详细的学科意愿调查,记抽到的3人中选择化学的有X人,求随机变量X的分布列及数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() 是定义域为R的奇函数,其中m是常数.
是定义域为R的奇函数,其中m是常数.
(Ⅰ)判断f(x)的单调性,并用定义证明;
(Ⅱ)若对任意x∈[﹣3,1],有f(tx)+f(2t﹣1)≤0恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离
的距离![]() ,倾斜角为
,倾斜角为![]() 的直线经过焦点
的直线经过焦点![]() ,且与抛物线交于两点
,且与抛物线交于两点![]() 、
、![]() .
.
(1)求抛物线的标准方程及准线方程;
(2)若![]() 为锐角,作线段
为锐角,作线段![]() 的中垂线
的中垂线![]() 交
交![]() 轴于点
轴于点![]() .证明:
.证明:![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com