
“a=1”是“(1+ax)6的展开式的各项系数之和为64”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
科目:高中数学 来源: 题型:
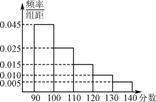
某市高三数学抽样考试中,对90分及其以上的成绩情况进行统计,其频率分布直方图如右下图所示,若(130,140]分数段的人数为90人,则(90,100]分数段的人数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
根据下图所示的伪代码,输出的结果T为________.
T←1
I←3
While I<20
T←T+Ⅰ
I←I+2
End While
Print T
查看答案和解析>>
科目:高中数学 来源: 题型:
下列有关命题的说法正确的是( )
A.命题“若x=y,则sin x=sin y”的逆否命题为真命题
B.函数f(x)=tan x的定义域为{x|x≠kπ,k∈Z}
C.命题“∃x∈R,使得x2+x+1<0”的否定是:“∀x∈R,均有x2+x+1<0”
D.“a=2”是“直线y=-ax+2与y=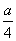 x-1垂直”的必要不充分条件
x-1垂直”的必要不充分条件
A 命题立意:本题考查常用逻辑用语的有关知识,难度较小.
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列命题:
①α=β是tan α=tan β的既不充分也不必要条件;
②“p为真”是“p且q为真”的必要不充分条件;
③数列{an}为等比数列是数列{anan+1}为等比数列的充分不必要条件;
④a=2是f(x)=|x-a|在[2,+∞)上为增函数的充要条件.
其中真命题的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知三棱锥S-ACB的四个顶点都在半径为1的球面上,底面△ABC是正三角形,SA=SB=SC,且平面ABC过球心,则三棱锥S-ABC的体积是( )
A.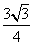 B.
B.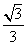 C.
C. D.
D.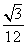
查看答案和解析>>
科目:高中数学 来源: 题型:
已知正三角形ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是________.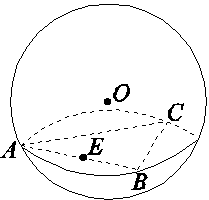
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,过圆E外一点A作一条直线与圆E交于B,C两点,且AB=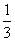 AC,作直线AF与圆E相切于点F,连接EF交BC于点D,已知圆E的半径为2,∠EBC=30°.
AC,作直线AF与圆E相切于点F,连接EF交BC于点D,已知圆E的半径为2,∠EBC=30°.
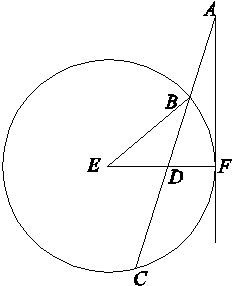
(1)求AF的长;
(2)求证:AD=3ED.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com