
分析 (1)把C角用A,B角表示,结合诱导公式解题;(2)利用第一小问的结论,面积公式$\frac{1}{2}absinC$计算即可.
解答 解:(1)∵$;A=\frac{π}{2}+\\;C$A=$\frac{π}{2}$+C,
∴sinA=cosC,cosA=-sinC,
∵sinB=$\frac{3}{5}$,
∴$cosB=\frac{4}{5}$,
cosC=-cos(A+B)=-cosAcosB+sinAsinB,
cosC=$\frac{4}{5}sinC$+$\frac{3}{5}cosC$,
tanC=$\frac{1}{2}$∴$cosC=\frac{2\sqrt{5}}{5}$;
(2)∵$a+c=3\sqrt{5}$,
∴$2R(sinA+sinC)=3\sqrt{5}$,
2R=5,a=2RsinA=2$\sqrt{5}$,b=2RsinB=3,
S=$\frac{1}{2}\\;absinC=\frac{3\sqrt{5}}{5}$.
点评 本题考查了正弦定理,两角和差的正弦函数,同角三角函数的关系


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:解答题
 如图,正方形ABCD边长为2,以A为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连接BF并延长交CD于点E.
如图,正方形ABCD边长为2,以A为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连接BF并延长交CD于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
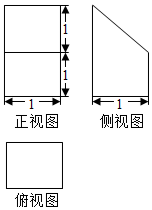 某几何体的三视图如图所示,则该几何体的表面积等于( )
某几何体的三视图如图所示,则该几何体的表面积等于( )| A. | 7+$\sqrt{2}$ | B. | 6+$\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 身高/cm(x) | 150 | 155 | 160 | 165 | 170 |
| 体重/kg(y) | 43 | 46 | 49 | 51 | 56 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com