
分析 (1)求出函数的导数,通过讨论m的范围,确定函数的单调性;
(2)求出g(x)的导数,通过讨论m的范围,求出函数的单调区间,从而求出函数的最值,判断是否符合题意,从而判断出m的范围即可.
解答 解:(1)由已知得mx+1>0,f′(x)=$\frac{m}{mx+1}$,
①若m>0时,由mx+1>0,得:x>-$\frac{1}{m}$,恒有f′(x)>0,
∴f(x)在(-$\frac{1}{m}$,+∞)递增;
②若m<0,由mx+1>0,得:x<-$\frac{1}{m}$,恒有f′(x)<0,
∴f(x)在(-∞,-$\frac{1}{m}$)递减;
综上,m>0时,f(x)在(-$\frac{1}{m}$,+∞)递增,
m<0时,f(x)在(-∞,-$\frac{1}{m}$)递减;
(2)g(x)=ln(mx+1)+$\frac{4}{x+2}$-2,(m>0),
∴g′(x)=$\frac{{mx}^{2}+4m-4}{(mx+1{)(x+2)}^{2}}$,
令h(x)=mx2+4m-4,
m≥1时,h(x)≥0,g′(x)≥0,g(x)无极值点,
0<m<1时,令h(x)=0,得:x1=-2$\sqrt{\frac{1}{m}-1}$或x2=2$\sqrt{\frac{1}{m}-1}$,
由g(x)的定义域可知x>-$\frac{1}{m}$且x≠-2,
∴-2$\sqrt{\frac{1}{m}-1}$>-$\frac{1}{m}$且-2$\sqrt{\frac{1}{m}-1}$≠-2,解得:m≠$\frac{1}{2}$,
∴x1,x2为g(x)的两个极值点,
即x1=-2$\sqrt{\frac{1}{m}-1}$,x2=2$\sqrt{\frac{1}{m}-1}$,
且x1+x2=0,x1•x2=$\frac{4(m-1)}{m}$,得:
g(x1)+g(x2)=ln(mx1+1)+$\frac{4}{{x}_{2}+2}$-2+ln(mx2+1)+$\frac{4}{{x}_{2}+2}$-2
=ln(2m-1)2+$\frac{2}{2m-1}$-2,
令t=2m-1,F(t)=lnt2+$\frac{2}{t}$-2,
①0<m<$\frac{1}{2}$时,-1<t<0,
∴F(t)=2ln(-t)+$\frac{2}{t}$-2,
∴F′(t)=$\frac{2(t-1)}{{t}^{2}}$<0,
∴F(t)在(-1,0)递减,F(t)<F(-1)<0,
即0<m<$\frac{1}{2}$时,g(x1)+g(x2)<0成立,符合题意;
②$\frac{1}{2}$<m<1时,0<t<1,
∴F(t)=2lnt+$\frac{2}{t}$-2,F′(t)=$\frac{2(t-1)}{{t}^{2}}$<0,
∴F(t)在(0,1)递减,F(t)>F(1)=0,
∴$\frac{1}{2}$<m<1时,g(x1)+g(x2)>0,不合题意,
综上,m∈(0,$\frac{1}{2}$).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,考查分类讨论思想,是一道综合题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 如图,在菱形ABCD中,∠BAD=60°,平面BDEF⊥平面ABCD,四边形BDEF是正方形,点M在线段EF上,$\overrightarrow{EM}$=λ$\overrightarrow{EF}$.
如图,在菱形ABCD中,∠BAD=60°,平面BDEF⊥平面ABCD,四边形BDEF是正方形,点M在线段EF上,$\overrightarrow{EM}$=λ$\overrightarrow{EF}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 有骨质疏松症状 | 无骨质疏松症状 | 总计 | |
| 常喝碳酸饮料的同学 | 22 | 8 | 30 |
| 不常喝碳酸饮料的同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
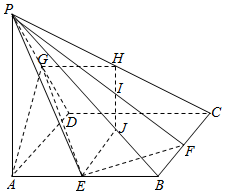 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,点E、F、G分别为棱AB、BC、PD的中点,平面AEG与线段PC、PF、PB分别交于点H、I、J,且PA=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,点E、F、G分别为棱AB、BC、PD的中点,平面AEG与线段PC、PF、PB分别交于点H、I、J,且PA=AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com