
 一光源在点M(
一光源在点M( ,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,折射后又射向抛物线上的点Q,再折射后,又沿平行于抛物线的轴的方向射出,途中遇到直线l: 2x-4y-17=0上的点N,再折射后又射回点M(如下图所示)
,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,折射后又射向抛物线上的点Q,再折射后,又沿平行于抛物线的轴的方向射出,途中遇到直线l: 2x-4y-17=0上的点N,再折射后又射回点M(如下图所示)
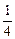 ,-1)与点M关于直线PN对称.
,-1)与点M关于直线PN对称.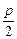 ,0),
,0),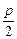 ) ①
) ①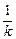 y+
y+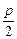 ,将其代入抛物线方程y2=2px中,整理,得y2-
,将其代入抛物线方程y2=2px中,整理,得y2-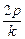 y-p2=0,由韦达定理,y1y2=-p2。
y-p2=0,由韦达定理,y1y2=-p2。 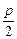 代入抛物线方程,得y=±p,同样得到y1·y2=-p2.
代入抛物线方程,得y=±p,同样得到y1·y2=-p2.  ,4)关于l的对称点为M′(x′,y′),则
,4)关于l的对称点为M′(x′,y′),则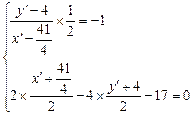 解得
解得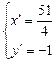
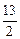 ,
,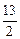 ,-1)
,-1)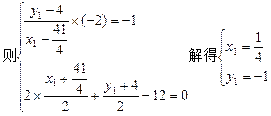
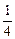 ,-1)的坐标是抛物线方程y2=4x的解,故抛物线上存在一点(
,-1)的坐标是抛物线方程y2=4x的解,故抛物线上存在一点(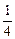 ,-1)与点M关于直线PN对称.
,-1)与点M关于直线PN对称.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 相交于B、C两点,点
相交于B、C两点,点
 轴上的射影分别为
轴上的射影分别为 , P是线段BC上的点,且适合
, P是线段BC上的点,且适合 ,求
,求 的重心Q的轨迹方程,并说明该轨迹是什么图形.
的重心Q的轨迹方程,并说明该轨迹是什么图形.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
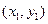 ,C
,C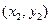 都在抛物线
都在抛物线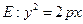 上,△ABC的重心与此抛物线E的焦点F重合. (1)写出抛物线E的方程及焦点坐标; (2)求线段BC的中点M的坐标及BC边所在的直线方程.
上,△ABC的重心与此抛物线E的焦点F重合. (1)写出抛物线E的方程及焦点坐标; (2)求线段BC的中点M的坐标及BC边所在的直线方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
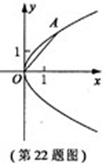
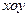 中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在
中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在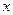 轴上。
轴上。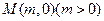 的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为
的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为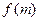 ,求
,求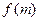 关于
关于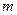 的表达式。
的表达式。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com