
已知抛物线C:y2=4x的焦点为F,直线y=2x-4与C交于A、B两点,则cos∠AFB=( )
A.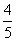 B.
B.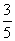
C.-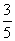 D.-
D.-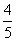
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,圆C1,直线C2的极坐标方程分别为ρ=4sinθ,ρcos(θ-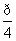 )=2
)=2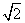 .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点.已知直线PQ的参数方程为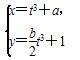 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
不等式(1+x)(1-|x|)>0的解集是( )
A.{x|0≤x<1} B.{x|x<0且x≠-1}
C.{x|-1<x<1} D.{x|x<1且x≠-1}
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆的中心是坐标原点O,焦点F1,F2在y轴上,它的一个顶点为A(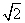 ,0),且中心O到直线AF1的距离为焦距的
,0),且中心O到直线AF1的距离为焦距的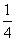 ,过点M(2,0)的直线l与椭圆交于不同的两点P,Q,点N在线段PQ上.
,过点M(2,0)的直线l与椭圆交于不同的两点P,Q,点N在线段PQ上.
(1)求椭圆的标准方程;
(2)设|PM|·|NQ|=|PN|·|MQ|,求动点N的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com