
【题目】定义在R上的函数f(x)满足对任意x,y∈R恒有f(xy)=f(x)+f(y),且f(x)不恒为0,
(1)求f(1)和f(﹣1)的值;
(2)试判断f(x)的奇偶性,并加以证明;
(3)若x≥0时f(x)为增函数,求满足不等式f(x+1)﹣f(2﹣x)≤0的x取值集合.
【答案】
(1)解:令x=y=1,得f(1)=f(1)+f(1)=2f(1),
∴f(1)=0,
令x=y=﹣1,得f(1)=f(﹣1)+f(﹣1)=2f(﹣1)=0,
∴f(﹣1)=0
(2)解:令y=﹣1,则f(﹣x)=f(x)+f(﹣1)=f(x),
∴f(﹣x)=f(x)
∴f(x)是偶函数
(3)解:由式f(x+1)﹣f(2﹣x)≤0得式f(x+1)≤f(2﹣x),
由(2)函数是偶函数,
则不等式等价为f(|x+1|)≤f(|2﹣x|),
∵x≥0时f(x)为增函数,
∴不等式等价为|x+1|≤|2﹣x|,
平方得x2+2x+1≤x2﹣4x+4,
即6x≤3,即x≤ ![]() ,
,
即满足不等式f(x+1)﹣f(2﹣x)≤0的x取值集合为(﹣∞, ![]() ]
]
【解析】(1)利用赋值法即可求f(1)、f(﹣1)的值;(2)根据函数奇偶性的定义即可证明f(x)是偶函数;(3)根据函数奇偶性和单调性的关系将不等式进行转化求解即可.


科目:高中数学 来源: 题型:
【题目】如图是某校举行歌唱比赛时,七位评委为某位选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的中位数和平均数依次为( ) 
A.87,86
B.83,85
C.88,85
D.82,86
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)定义域中任意的x1 , x2(x1≠x2),有如下结论:
(1)f(x1+x2)=f(x1)f(x2)
(2)f(x1x2)=f(x1)+f(x2)
(3) ![]()
当f(x)=ex时,上述结论中正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面几何中有如下结论:正三角形ABC的内切圆面积为S1 , 外接圆面积为S2 , 则 ![]() ,推广到空间可以得到类似结论;已知正四面体P﹣ABC的内切球体积为V1 , 外接球体积为V2 , 则
,推广到空间可以得到类似结论;已知正四面体P﹣ABC的内切球体积为V1 , 外接球体积为V2 , 则 ![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x∈R,定义符号函数sgnx= 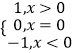 ,则( )
,则( )
A.|x|=x|sgnx|
B.|x|=xsgn|x|
C.|x|=|x|sgnx
D.|x|=xsgnx
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P是圆x2+y2=4上一动点,PD⊥x轴于点D,记满足 ![]() =
= ![]() (
( ![]() +
+ ![]() )的动点M的轨迹为Γ. (Ⅰ)求轨迹Γ的方程;
)的动点M的轨迹为Γ. (Ⅰ)求轨迹Γ的方程;
(Ⅱ)已知直线l:y=kx+m与轨迹F交于不同两点A,B,点G是线段AB中点,射线OG交轨迹Γ于点Q,且 ![]() =λ
=λ ![]() ,λ∈R.
,λ∈R.
①证明:λ2m2=4k2+1;
②求△AOB的面积S(λ)的解析式,并计算S(λ)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知acosB+bcosA=2ccosC.
(1)求角C的大小;
(2)若a=5,b=8,求边c的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com