
在△ABC中,∠ABC=60°,AB=2,BC=3,在BC上任取一点D,使△ABD为钝角三角形的概率为( )
A.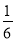 B.
B.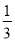 C.
C.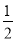 D.
D.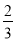
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2015届高考苏教数学训练3 简单的逻辑联结词、全称量词与存在量词(解析版) 题型:填空题
【已知命题p1:存在x0∈R,使得x02+x0+1<0成立;p2:对任意x∈[1,2],x2-1≥0.以下命题:
①( p1)∧(
p1)∧( p2);②p1∨(
p2);②p1∨( p2);③(
p2);③( p1)∧p2;④p1∧p2.
p1)∧p2;④p1∧p2.
其中为真命题的是________(填序号).
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破四 高考立体几何(解析版) 题型:选择题
某几何体的三视图如图所示,则它的体积是( )
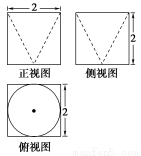
A.8-2π B.8-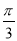 C.8-
C.8-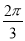 D.
D.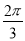
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破六 高考概率与统计(解析版) 题型:填空题
从n个正整数1,2,…,n中任意取出两个不同的数,若取出的两数之和等于5的概率为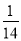 ,则n=________.
,则n=________.
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破五 高考解析几何(解析版) 题型:解答题
已知曲线E上任意一点P到两个定点F1(-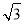 ,0)和F2(
,0)和F2(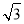 ,0)的距离之和为4.
,0)的距离之和为4.
(1)求曲线E的方程;
(2)设过点(0,-2)的直线l与曲线E交于C、D两点,且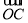 ·
·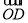 =0(O为坐标原点),求直线l的方程.
=0(O为坐标原点),求直线l的方程.
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破五 高考解析几何(解析版) 题型:选择题
已知点M(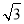 ,0),椭圆
,0),椭圆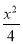 +y2=1与直线y=k(x+
+y2=1与直线y=k(x+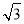 )交于点A、B,则△ABM的周长为( )
)交于点A、B,则△ABM的周长为( )
A.4 B.8 C.12 D.16
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破三 高考数列(解析版) 题型:解答题
在等差数列{an}中,a1+a3=8,且a4为a2和a9的等比中项,求数列{an}的首项、公差及前n项和.
查看答案和解析>>
科目:高中数学 来源:2015届陕西省西安市高二下学期期末考试文科数学试卷(解析版) 题型:解答题
已知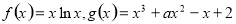
(1)如果函数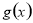 的单调递减区间为
的单调递减区间为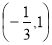 ,求函数
,求函数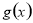 的解析式;
的解析式;
(2)对一切的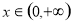 ,
,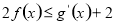 恒成立,求实数
恒成立,求实数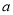 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com