
已知函数f(x)=x3-x2+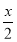 +
+ .
.
证明:存在x0∈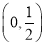 ,使f(x0)=x0.
,使f(x0)=x0.
科目:高中数学 来源:2015届高考苏教数学(理)训练18 同角三角函数的基本关系与诱导公式(解析版) 题型:解答题
如图,单位圆(半径为1的圆)的圆心O为坐标原点,单位圆与y轴的正半轴交于点A,与钝角α的终边OB交于点B(xB,yB),设∠BAO=β.
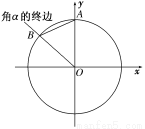
(1)用β表示α;
(2)如果 sin β= ,求点B(xB,yB)坐标;
,求点B(xB,yB)坐标;
(3)求xB-yB的最小值.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练15 导数与函数极值、最值(解析版) 题型:填空题
已知函数y=f(x)=x3+3ax2+3bx+c在x=2处有极值,其图像在x=1处的切线平行于直线6x+2y+5=0,则f(x)极大值与极小值之差为________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练13 变化率与导数、导数的计算(解析版) 题型:解答题
已知函数f(x)=x2-(1+2a)x+aln x(a为常数).
(1)当a=-1时,求曲线y=f(x)在x=1处切线的方程;
(2)当a>0时,讨论函数y=f(x)在区间(0,1)上的单调性,并写出相应的单调区间.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练13 变化率与导数、导数的计算(解析版) 题型:填空题
曲线y=x3+ax+1的一条切线方程为y=2x+1,则实数a=________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练11 函数与方程(解析版) 题型:填空题
若函数f(x)=-|x-5|+2x-1的零点所在的区间是(k,k+1),则整数k=________.
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破六 高考概率与统计(解析版) 题型:选择题
在△ABC中,∠ABC=60°,AB=2,BC=3,在BC上任取一点D,使△ABD为钝角三角形的概率为( )
A.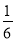 B.
B.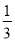 C.
C.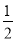 D.
D.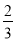
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com