练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．如图，M是抛物线y2=4x上一点（M在x轴上方），F是抛物线的焦点，若|FM|=4，则∠xFM=（　　）
    A．30°B．45°C．60°D．75°

    分析 利用抛物线的性质求出M的坐标，求出FM的斜率，即可求解∠xFM．

    解答 解：由题意抛物线y2=4x得F（1，0），M是抛物线y2=4x上一点（M在x轴上方），
    |FM|=4，可得M（3，2$\sqrt{3}$）．
    ∴MF的斜率为：$\frac{2\sqrt{3}-0}{3-1}$=$\sqrt{3}$，
    tan∠xFM=$\sqrt{3}$．
    ∠xFM=60°．
    故选：C．

    点评 本题考查抛物线的简单性质的应用，解决此类问题关键是灵活运用抛物线的定义，将问题转化为我们熟悉的平面几何知识．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    17．（1）构造函数证明不等式的性质，若a＞b＞0，则$\frac{1}{a}＜\frac{1}{b}$．
    （2）求证：x＞2时，x3-6x2+12x-1＞7．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．以一年为一个调查期，在调查某商品出厂价格及销售价格时发现：每件商品的出厂价格是在6元基础上按月份随正弦型函数曲线波动，已知3月份出厂价格最高为8元，7月份出厂价格最低为4元，而每件商品的销售价格是在8元基础上同样按月份随正弦型函数曲线波动，且5月份销售价格最高为10元，9月份销售价格最低为6元，假设某商店每月购进这种商品m件，且当月售完，则该商店的月毛利润的最大值为6元．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知抛物线y2=2px（p＞0）的准线与x轴的交点为Q，过点Q的直线与抛物线相切于点P，F是抛物线的焦点，若△PQF的面积为8，则P的值为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．设f（x）是定义域R上的函数，且f（0）=1，对任意x，y∈R，恒有f（x-y）=f（x）-y（2x-y+1），求f（x）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

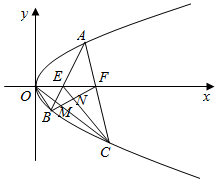    12．如图，点A（x1，y1），B（x2，y2），C（x3，y3）（y1＞0，y2＜0，y3＜0）是抛物线y2=2px（p＞0）上不同三点，AB，AC分别与x轴交于点E、F，BF与OC，EC分别交于M，N，则（　　）
    A．S△OBM=S△ENF+S△MNCB．S△OBM=S△ENF-S△MNC
    C．S△OBM+S△ENF=S△MNCD．S△OBM+S△ENF=2S△MNC

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．函数y=2$\sqrt{2-x}$+$\sqrt{2x-3}$的最大值为$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．交通指数是交通拥堵指数的简称，是综合反映某区域道路网在某特定时段内畅通或拥堵实际情况的概念性指数值．交通指数范围为（0，10），五个级别规定如下：
    交通指数（0，2）[2，4）[4，6）[6，8）[8，10）
    级别畅通基本畅通轻度拥堵中度拥堵严重拥堵
    某人在工作日上班出行每次经过的路段都在同一个区域内，他随机记录了上班的40个工作日早高峰时段（早晨7点至9点）的交通指数（平均值），其统计结果如直方图所示．
    （Ⅰ）据此估计此人260个工作日中早高峰时段（早晨7点至9点）中度拥堵的天数；
    （Ⅱ）若此人早晨上班路上所用时间近似为：畅通时30分钟，基本畅通时35分钟，轻度拥堵时40分钟，中度拥堵时50分钟，严重拥堵时70分钟，以直方图中各种路况的频率作为每天遇到此种路况的概率，求此人上班路上所用时间X的数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．设集合A={x∈Z|0≤x＜3}，集合B={x∈Z|x2≤1}，则A∩B=（　　）
    A．{0，1，2}B．{0，1}C．[0，1]D．{-1，0，1，2}

    查看答案和解析>>

    同步练习册答案