
分析 由题意,Q(-$\frac{p}{2}$,0),F($\frac{p}{2}$,0),设P(a,b),利用△PQF的面积为8,求出P的坐标,求出抛物线在P的切线方程,Q(-$\frac{p}{2}$,0),代入可得0-$\frac{16}{p}$=$\frac{p}{\frac{16}{p}}$(-$\frac{p}{2}$-$\frac{128}{{p}^{3}}$),解方程,可得p的值.
解答 解:由题意,Q(-$\frac{p}{2}$,0),F($\frac{p}{2}$,0),设P(a,b),
∵△PQF的面积为8,
∴$\frac{1}{2}×p×|b|$=8,
∴|b|=$\frac{16}{p}$,∴a=$\frac{128}{{p}^{3}}$,
取P($\frac{128}{{p}^{3}}$,$\frac{16}{p}$),则抛物线在P的切线方程为y-$\frac{16}{p}$=$\frac{p}{\frac{16}{p}}$(x-$\frac{128}{{p}^{3}}$),
Q(-$\frac{p}{2}$,0),代入可得0-$\frac{16}{p}$=$\frac{p}{\frac{16}{p}}$(-$\frac{p}{2}$-$\frac{128}{{p}^{3}}$),
∴p=4.
故答案为:4.
点评 本题考查抛物线的方程与性质,考查直线与抛物线的位置关系,考查抛物线的切线方程,考查学生的计算能力,属于中档题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:解答题
 如图,已知直线l与抛物线y2=2x相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,若y1y2=-4,
如图,已知直线l与抛物线y2=2x相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,若y1y2=-4,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
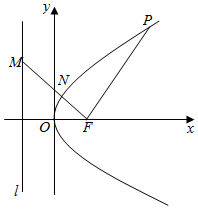 如图,P为抛物线C:y2=8x上一点,F为抛物线的焦点,M为抛物线准线l上一点,且MF⊥PF,线段MF与抛物线交于点N,若|PF|=8,则$\frac{|MN|}{|NF|}$=( )
如图,P为抛物线C:y2=8x上一点,F为抛物线的焦点,M为抛物线准线l上一点,且MF⊥PF,线段MF与抛物线交于点N,若|PF|=8,则$\frac{|MN|}{|NF|}$=( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{2}{3}$$\sqrt{3}$ | D. | $\frac{3}{2}$$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
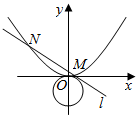 过抛物线L:x2=2py(p>0)的焦点F且斜率为$\frac{3}{4}$的直线与抛物线L在第一象限的交点为P,且|PF|=5.
过抛物线L:x2=2py(p>0)的焦点F且斜率为$\frac{3}{4}$的直线与抛物线L在第一象限的交点为P,且|PF|=5.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5\sqrt{2}}{6}$ | B. | 3$\sqrt{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com