
分析 分别求出出厂价波动函数和售价波动函数,求出每件盈利的表达式,利用正弦函数的性质即可求出最大值.
解答 解:设函数y1=Asin(ωx+α)+B,
∵函数在6元基础上按月份随正弦曲线波动的,
∴B=6,
又∵3月份出厂价格最高为8元,7月份出厂价格最低为4元,
∴A=2,T=2×(7-3)=8,
∴$ω=\frac{π}{4}$;
即${y}_{1}=2sin(\frac{π}{4}x+α)+6$;
将(3,8)点代入函数解析式得:$α=-\frac{π}{4}$;
又${y}_{1=}2sin(\frac{π}{4}x-\frac{3π}{4})+8$同时在8元的基础上按月份也是随正弦曲线波动的,
并已知5月份销售价格最高为10元,9月份销售价格最低为6元,
可得${y}_{2}=2sin(\frac{π}{4}x-\frac{3π}{4})+8$;
每件盈利y=m(y2-y1)
=$(-2\sqrt{2}sin\frac{π}{4}x+2)m$,
当sin$\frac{π}{4}$x=-1,即$\frac{π}{4}$x=2kπ-$\frac{π}{2}$时,
解答x=8k-2,k∈Z;
∴当k=1时,估计出6月份盈利最大.
故答案为:6.
点评 本题考查了正弦函数模型的应用问题,也考查了利用正弦函数的性质求最值的应用问题,是综合性题目.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
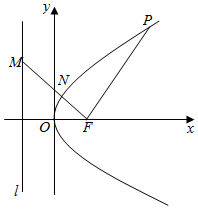 如图,P为抛物线C:y2=8x上一点,F为抛物线的焦点,M为抛物线准线l上一点,且MF⊥PF,线段MF与抛物线交于点N,若|PF|=8,则$\frac{|MN|}{|NF|}$=( )
如图,P为抛物线C:y2=8x上一点,F为抛物线的焦点,M为抛物线准线l上一点,且MF⊥PF,线段MF与抛物线交于点N,若|PF|=8,则$\frac{|MN|}{|NF|}$=( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{2}{3}$$\sqrt{3}$ | D. | $\frac{3}{2}$$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com