练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    根据下列条件，求双曲线方程．

    (1)与双曲线＝1有共同的渐近线，且过点(－3，2)；

    (2)与双曲线＝1有公共焦点，且过点(3，2)．

     

    （1）＝1.（2）＝1

    【解析】解法1：(1)设双曲线的方程为＝1，

    由题意，得

    解得a2＝，b2＝4. 所以双曲线的方程为＝1.

    (2)设双曲线方程为＝1.由题意易求得c＝2.

    又双曲线过点(3，2)，∴＝1.又∵a2＋b2＝(2)2，∴a2＝12，b2＝8.

    故所求双曲线的方程为＝1.

    解法2：(1)设所求双曲线方程为＝λ(λ≠0)，

    将点(－3，2)代入得λ＝，所以双曲线方程为＝.

    (2)设双曲线方程为＝1，

    将点(3，2)代入得k＝4，所以双曲线方程为＝1.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第十一章第5课时练习卷（解析版） 题型：解答题

    设进入某商场的每一位顾客购买甲种商品的概率为0.5，购买乙种商品的概率为0.6，且购买甲种商品与购买乙种商品相互独立，各顾客之间购买商品也是相互独立的．

    (1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率；

    (2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率；

    (3)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数，求ξ的分布列．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第十一章第3课时练习卷（解析版） 题型：解答题

    如果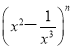的展开式中，第四项和第七项的二项式系数相等，求：

    (1)展开式的中间项；

    (2)展开式中所有的有理项．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第九章第9课时练习卷（解析版） 题型：填空题

    抛物线y＝－x2上的点到直线4x＋3y－8＝0的距离的最小值是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第九章第9课时练习卷（解析版） 题型：填空题

    抛物线y2＝4x上一点M到焦点的距离为3，则点M的横坐标x＝________．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第九章第8课时练习卷（解析版） 题型：填空题

    已知双曲线＝1的右焦点为(3，0)，则该双曲线的离心率为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第九章第8课时练习卷（解析版） 题型：解答题

    已知双曲线的焦点在x轴上，两个顶点间的距离为2，焦点到渐近线的距离为.

    (1)求双曲线的标准方程；

    (2)写出双曲线的实轴长、虚轴长、焦点坐标、离心率、渐近线方程．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第九章第7课时练习卷（解析版） 题型：解答题

    已知曲线C：(5－m)x2＋(m－2)y2＝8(m∈R)．

    (1)若曲线C是焦点在x轴上的椭圆，求m的取值范围；

    (2)设m＝4，曲线C与y轴的交点为A，B(点A位于点B的上方)，直线y＝kx＋4与曲线C交于不同的两点M，N，直线y＝1与直线BM交于点G.求证：A，G，N三点共线．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第九章第5课时练习卷（解析版） 题型：填空题

    已知直线l过点(－2，0)，当直线l与圆x2＋y2＝2x有两个交点时，其斜率k的取值范围是________．

     

    查看答案和解析>>

    同步练习册答案