
ĄŸÌâÄżĄżÄł”Ű·œŐțžźÒȘœ«Ò»żéÈçÍŒËùÊŸ”ÄÖ±œÇÌĘĐÎABCDżŐ”ŰžÄœšÎȘœĄÉíÓéÀÖč㳥.ÒŃÖȘAD//BC, ![]() °ÙĂŚŁŹ
°ÙĂŚŁŹ ![]() °ÙĂŚŁŹč㳥ÈëżÚPÔÚABÉÏŁŹÇÒ
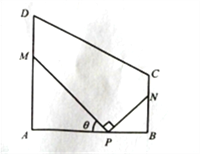
°ÙĂŚŁŹč㳥ÈëżÚPÔÚABÉÏŁŹÇÒ![]() ŁŹžùŸĘčæ»źŁŹčę”ăPÆÌÉèÁœÌőÏໄŽčÖ±”ıÊֱХ·PM,PNŁšĐĄÂ·”Äżí¶ÈČ»ŒÆŁ©ŁŹ”ăM,N·Ö±đÔÚ±ßAD,BCÉÏŁš°üșŹ¶Ë”㣩ŁŹ
ŁŹžùŸĘčæ»źŁŹčę”ăPÆÌÉèÁœÌőÏໄŽčÖ±”ıÊֱХ·PM,PNŁšĐĄÂ·”Äżí¶ÈČ»ŒÆŁ©ŁŹ”ăM,N·Ö±đÔÚ±ßAD,BCÉÏŁš°üșŹ¶Ë”㣩ŁŹ![]() ÇűÓòÄ✚ÎȘÌűÎèœĄÉíč㳥ŁŹ
ÇűÓòÄ✚ÎȘÌűÎèœĄÉíč㳥ŁŹ ![]() ÇűÓòÄ✚ÎȘ¶ùÍŻÀÖÔ°ŁŹÆäËüÇűÓòÆÌÉèÂÌ»ŻČĘÆșŁŹÉè
ÇűÓòÄ✚ÎȘ¶ùÍŻÀÖÔ°ŁŹÆäËüÇűÓòÆÌÉèÂÌ»ŻČĘÆșŁŹÉè![]() .
.
Łš1Ł©ÇóÂÌ»ŻČĘÆșĂæ»ę”ÄŚîŽóÖ”Ł»
Łš2Ł©ÏÖÄ✫ÁœÌőХ·PNM,PNœűĐĐȻ͏·çžń”ÄĂÀ»ŻŁŹPMХ·”ÄĂÀ»Ż·ŃÓĂÎȘĂż°ÙĂŚ1ÍòÔȘŁŹPNХ·”ÄĂÀ»Ż·ŃÓĂÎȘĂż°ÙĂŚ2ÍòÔȘŁŹÊÔÈ·¶šM,N”ÄλÖĂŁŹÊč”ĂХ·PM,PN”ÄĂÀ»ŻŚÜ·ŃÓĂŚî”ÍŁŹČąÇółöŚîĐĄ·ŃÓĂ.
ĄŸŽđ°žĄż(1) ÂÌ»ŻČĘÆșĂæ»ę”ÄŚîŽóÖ”ÎȘ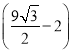 Æœ·œ°ÙĂŚ;(2)
Æœ·œ°ÙĂŚ;(2) ![]() ʱŚÜĂÀ»Ż·ŃÓĂŚî”ÍÎȘ4ÍòÔȘ.
ʱŚÜĂÀ»Ż·ŃÓĂŚî”ÍÎȘ4ÍòÔȘ.
ĄŸœâÎöĄżÊÔÌâ·ÖÎöŁșŁš1Ł©ÏÈÇó”Ă![]()
![]() ,ÔÙÀûÓĂŸù֔Ȼ”ÈÊœÇó”ĂŐęœâŁ»Łš2Ł©ÏÈÇó”Ă
,ÔÙÀûÓĂŸù֔Ȼ”ÈÊœÇó”ĂŐęœâŁ»Łš2Ł©ÏÈÇó”Ă![]() ŁŹ
ŁŹ ![]()
ŚÜĂÀ»Ż·ŃÓĂÎȘ![]() ŁŹÔÙÀûÓĂ”ŒÊęč€ŸßÇó”ĂŐęœâ.
ŁŹÔÙÀûÓĂ”ŒÊęč€ŸßÇó”ĂŐęœâ.
ÊÔÌâœâÎöŁșŁš1Ł©ÔÚ![]() ÖĐŁŹ
ÖĐŁŹ ![]() ŁŹ”Ă
ŁŹ”Ă![]() ŁŹ
ŁŹ
ËùÒÔ![]()
ÓÉ![]() ,
,![]()
ÔÚ![]() ÖĐŁŹ
ÖĐŁŹ ![]() ŁŹ”Ă
ŁŹ”Ă![]() ŁŹ
ŁŹ
ËùÒÔ![]()
ËùÒÔÂÌ»ŻČĘÆșĂæ»ę![]()
![]()
![]()
![]()
ÓÖÒòÎȘ![]()
”±ÇÒ”±![]() ŁŹŒŽ
ŁŹŒŽ![]() ĄŁŽËʱ
ĄŁŽËʱ![]()
ËùÒÔÂÌ»ŻČĘÆșĂæ»ę”ÄŚîŽóÖ”ÎȘ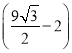 Æœ·œ°ÙĂŚ.
Æœ·œ°ÙĂŚ.
Łš2Ł©·œ·šÒ»ŁșÔÚ![]() ÖĐŁŹ
ÖĐŁŹ ![]() ŁŹ”Ă
ŁŹ”Ă![]() ŁŹ
ŁŹ
ÓÉ![]() ,
,![]()
ÔÚ![]() ÖĐŁŹ
ÖĐŁŹ ![]() ŁŹ”Ă
ŁŹ”Ă![]() ŁŹ
ŁŹ
ËùÒÔŚÜĂÀ»Ż·ŃÓĂÎȘ![]()
![]()
![]()
Áî![]() ”Ă
”Ă![]() ÁбíÈçÏÂ
ÁбíÈçÏÂ
|
|
|
|
|
|
| - | 0 | - | ||
|
| ”„”ś”ĘŒő |
| ”„”ś”ĘÔö |
|
ËùÒÔ”±![]() ʱŁŹŒŽ
ʱŁŹŒŽ![]() ʱŚÜĂÀ»Ż·ŃÓĂŚî”ÍÎȘ4ÍòÔȘĄŁ
ʱŚÜĂÀ»Ż·ŃÓĂŚî”ÍÎȘ4ÍòÔȘĄŁ
·œ·š¶țŁșÔÚ![]() ÖĐŁŹ
ÖĐŁŹ ![]() ŁŹ”Ă
ŁŹ”Ă![]() ŁŹ
ŁŹ
ÓÉ![]() ,
,![]()
ÔÚ![]() ÖĐŁŹ
ÖĐŁŹ ![]() ŁŹ”Ă
ŁŹ”Ă![]() ŁŹ
ŁŹ
ËùÒÔŚÜĂÀ»Ż·ŃÓĂÎȘ![]()
![]()
Áî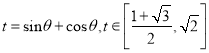 ”Ă
”Ă![]()
ËùÒÔ![]() ŁŹ
ŁŹ 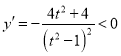
ËùÒÔ![]() ÔÚ
ÔÚ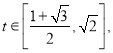 ÉÏÊÇ”„”ś”ĘŒő
ÉÏÊÇ”„”ś”ĘŒő
ËùÒÔ”±![]() ŁŹ
ŁŹ ![]() ʱŁŹŒŽ
ʱŁŹŒŽ![]() ʱŚÜĂÀ»Ż·ŃÓĂŚî”ÍÎȘ4ÍòÔȘĄŁ
ʱŚÜĂÀ»Ż·ŃÓĂŚî”ÍÎȘ4ÍòÔȘĄŁ


 ĂûÌâŃ”Á·Ï”ÁĐŽđ°ž
ĂûÌâŃ”Á·Ï”ÁĐŽđ°ž ÆÚÄ©ŒŻœáșĆÏ”ÁĐŽđ°ž
ÆÚÄ©ŒŻœáșĆÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÉè![]() ”ÄÄÚœÇAŁŹBŁŹC”ĶԱ߷ֱđÎȘaŁŹbŁŹcŁŹ
”ÄÄÚœÇAŁŹBŁŹC”ĶԱ߷ֱđÎȘaŁŹbŁŹcŁŹ![]() ŁŹÇÒBÎȘ¶ÛœÇ,
ŁŹÇÒBÎȘ¶ÛœÇ,
(1)![]() Ł»Łš2Ł©Çó
Ł»Łš2Ł©Çó![]() ”ÄÈĄÖ”·¶Î§
”ÄÈĄÖ”·¶Î§
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłĐËÈ€ĐĄŚéÓûŃĐŸżÖçÒčÎÂČîŽóĐĄÓ뻌žĐĂ°ÈËÊę¶àÉÙÖźŒä”ÄčŰÏ”ŁŹËûĂÇ·Ö±đ”œÆűÏóŸÖÓëÄłÒœÔșłÂŒÁË1ÖÁ6ÔÂĂżÔÂ10șĆ”ÄÖçÒčÎÂČîÇéżöÓëÒò»ŒžĐĂ°¶űŸÍŐï”ÄÈËÊ꣏”Ă”œÈçÏ”ČÊÁÏŁș
žĂĐËÈ€ĐĄŚéÈ·¶š”ÄŃĐŸż·œ°žÊÇŁșÏÖŽÓŐâÁùŚéÊęŸĘÖĐŃĄÈĄ2ŚéŁŹÓĂÊŁÏ”Ä4ŚéÊęŸĘÇóÏßĐÔ»Űčé·œłÌŁŹÔÙÓñ»ŃĄÓĂ”Ä2ŚéÊęŸĘœűĐĐŒìŃé.
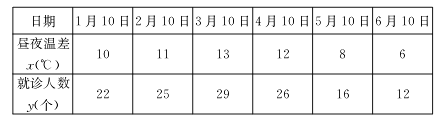
Łš1Ł©ÇóŃĄÈĄ”Ä2ŚéÊęŸĘÇĄșĂÊÇÏàÁÚÁœžöÔ”ĞĆÂÊŁ»
Łš2Ł©ÈôŃĄÈĄ”ÄÊÇ1ÔÂÓë6Ô”ÄÁœŚéÊęŸĘŁŹÇëžùŸĘ2ÖÁ5Ô”ÄÊęŸĘŁŹÇółö![]() čŰÓÚ
čŰÓÚ![]() ”ÄÏßĐÔ»Űčé·œłÌ
”ÄÏßĐÔ»Űčé·œłÌ![]() Ł»
Ł»
Łš3Ł©ÈôÓĐÏßĐÔ»Űčé·œłÌ”Ă”œ”ÄčÀŒÆÊęŸĘÓëËùŃĄłö”ÄŒìŃéÊęŸĘ”ÄÎóČîŸùČ»łŹčę2ÈËŁŹÔòÈÏÎȘ”Ă”œ”ÄÏßĐÔ»Űčé·œłÌÊÇÀíÏë”ÄŁŹÊÔÎÊŁš2Ł©ÖĐËù”ĂÏßĐÔ»Űčé·œłÌÊÇ·ńÊÇÀíÏ룿
ČÎżŒč«ÊœŁș
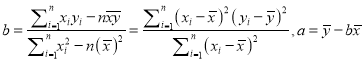
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈô¶šÒćÔÚ![]() ÉÏ”ÄșŻÊę
ÉÏ”ÄșŻÊę![]() ŁŹÆäÍŒÏóÊÇÁŹĐűČ»¶Ï”ÄŁŹÇÒŽæÔÚłŁÊę
ŁŹÆäÍŒÏóÊÇÁŹĐűČ»¶Ï”ÄŁŹÇÒŽæÔÚłŁÊę![]() Êč”Ă
Êč”Ă![]() ¶ÔÈÎÒâ”ÄÊ”Êę
¶ÔÈÎÒâ”ÄÊ”Êę![]() ¶ŒłÉÁąŁŹÔòłÆ
¶ŒłÉÁąŁŹÔòłÆ![]() ÊÇÒ»žöĄ°
ÊÇÒ»žöĄ°![]() ÌŰŐśșŻÊꥱÔòÏÂÁĐœáÂÛÖĐŐęÈ·”ÄžöÊęÎȘŁš Ł©Łź
ÌŰŐśșŻÊꥱÔòÏÂÁĐœáÂÛÖĐŐęÈ·”ÄžöÊęÎȘŁš Ł©Łź
ąÙ![]() ÊÇłŁÊęșŻÊęÖĐΚһ”ÄĄ°
ÊÇłŁÊęșŻÊęÖĐΚһ”ÄĄ°![]() ÌŰŐśșŻÊꥱŁ»
ÌŰŐśșŻÊꥱŁ»
ąÚ![]() Č»ÊÇĄ°
Č»ÊÇĄ°![]() ÌŰŐśșŻÊꥱŁ»
ÌŰŐśșŻÊꥱŁ»
ąÛĄ°![]() ÌŰŐśșŻÊꥱÖÁÉÙÓĐÒ»žöÁă”㣻
ÌŰŐśșŻÊꥱÖÁÉÙÓĐÒ»žöÁă”㣻
ąÜ![]() ÊÇÒ»žöĄ°
ÊÇÒ»žöĄ°![]() ÌŰŐśșŻÊꥱŁ»Łź
ÌŰŐśșŻÊꥱŁ»Łź
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÉèÊęÁĐ![]() ÂúŚă
ÂúŚă![]() ŁŹ
ŁŹ![]() .
.
Łš1Ł©Çó![]() Ł»
Ł»
Łš2Ł©ÏÈČÂÏëłö![]() ”ÄÒ»žöÍšÏîč«ÊœŁŹÔÙÓĂÊęѧčéÄÉ·šÖ€ĂśÄă”ÄČÂÏë.
”ÄÒ»žöÍšÏîč«ÊœŁŹÔÙÓĂÊęѧčéÄÉ·šÖ€ĂśÄă”ÄČÂÏë.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘșŻÊę![]() .
.
Łš1Ł©”±![]() ʱŁŹÇó
ʱŁŹÇó![]() ”Ä”„”śÇűŒäŁ»
”Ä”„”śÇűŒäŁ»
Łš2Ł©Èô¶Ô![]() ŁŹ¶ŒÓĐ
ŁŹ¶ŒÓĐ![]() łÉÁąŁŹÇó
łÉÁąŁŹÇó![]() ”ÄÈĄÖ”·¶Î§Ł»
”ÄÈĄÖ”·¶Î§Ł»
Łš3Ł©”±![]() ʱŁŹÇó
ʱŁŹÇó![]() ÔÚ
ÔÚ![]() ÉÏ”ÄŚîŽóÖ”.
ÉÏ”ÄŚîŽóÖ”.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘÖ±Ïßl1”Ä·œłÌÎȘ3x+4y©12=0Łź
Łš1Ł©ÈôÖ±Ïßl2Óël1ÆœĐĐŁŹÇÒčę”㣚©1ŁŹ3Ł©ŁŹÇóÖ±Ïßl2”Ä·œłÌŁ»
Łš2Ł©ÈôÖ±Ïßl2Óël1ŽčÖ±ŁŹÇÒl2ÓëÁœŚű±êÖáΧłÉ”ÄÈęœÇĐÎĂæ»ęÎȘ4ŁŹÇóÖ±Ïßl2”Ä·œłÌŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÉŁ»ùÓăÌÁÊÇÄł”ŰÒ»ÖÖ¶ÀŸß”Ű·œÌŰÉ«”ÄĆ©Ò”ÉúČúĐÎÊœŁŹÄłŃĐŸż”„λŽòËăżȘ·ąÒ»žöÉŁ»ùÓăÌÁÏîÄżŁŹžĂÏîÄżŚŒ±žčșÖĂÒ»żé![]() Æœ·œĂŚ”ÄŸŰĐΔۿ飏ÖĐŒäÍÚłÉÈęžöŸŰĐÎłŰÌÁŃűÓ㣏ÍÚłö”ÄÄàÍÁ¶ŃÔÚłŰÌÁËÄÖÜĐγɻùΧŁšÒőÓ°Čż·ÖËùÊŸŁ©ÖÖÖČÉŁÊśŁŹłŰÌÁÖÜΧ”Ä»ùΧżíŸùÎȘ
Æœ·œĂŚ”ÄŸŰĐΔۿ飏ÖĐŒäÍÚłÉÈęžöŸŰĐÎłŰÌÁŃűÓ㣏ÍÚłö”ÄÄàÍÁ¶ŃÔÚłŰÌÁËÄÖÜĐγɻùΧŁšÒőÓ°Čż·ÖËùÊŸŁ©ÖÖÖČÉŁÊśŁŹłŰÌÁÖÜΧ”Ä»ùΧżíŸùÎȘ![]() ĂŚŁŹÈçÍŒŁŹÉèłŰÌÁËùŐŒŚÜĂæ»ęÎȘ
ĂŚŁŹÈçÍŒŁŹÉèłŰÌÁËùŐŒŚÜĂæ»ęÎȘ![]() Æœ·œĂŚŁź
Æœ·œĂŚŁź
ŁšąńŁ©ÊÔÓĂ![]() ±íÊŸ
±íÊŸ![]() Łź
Łź
ŁšąòŁ©”±![]() ÈĄșÎ֔ʱŁŹČĆÄÜÊč”Ă
ÈĄșÎ֔ʱŁŹČĆÄÜÊč”Ă![]() ŚîŽóŁżČąÇółö
ŚîŽóŁżČąÇółö![]() ”ÄŚîŽóÖ”Łź
”ÄŚîŽóÖ”Łź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘșŻÊę![]()
(1)ÈôșŻÊę![]() ÔÚ¶šÒćÓòÄÚ”„”ś”ĘÔöŁŹÇóÊ”Êę
ÔÚ¶šÒćÓòÄÚ”„”ś”ĘÔöŁŹÇóÊ”Êę ![]() ”ÄÈĄÖ”·¶Î§ŁŹ
”ÄÈĄÖ”·¶Î§ŁŹ
(2)”±![]() ʱŁŹčŰÓÚ
ʱŁŹčŰÓÚ![]() ”Ä·œłÌ
”Ä·œłÌ![]() ÔÚ[1,4]ÉÏÇĄÓĐÁœžöČ»Ïà”È”ÄÊ”ÊęžùŁŹ
ÔÚ[1,4]ÉÏÇĄÓĐÁœžöČ»Ïà”È”ÄÊ”ÊęžùŁŹ
ÇóÊ”Êę”ÄÈĄÖ”·¶Î§ĄŁ
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com