
【题目】已知函数![]()
(1)若函数![]() 在定义域内单调递增,求实数
在定义域内单调递增,求实数 ![]() 的取值范围,
的取值范围,
(2)当![]() 时,关于
时,关于![]() 的方程
的方程![]() 在[1,4]上恰有两个不相等的实数根,
在[1,4]上恰有两个不相等的实数根,
求实数的取值范围。
【答案】(1) (﹣∞,﹣1];(2) ln2﹣2<b≤﹣![]()
【解析】试题分析:(1)对函数f(x)进行求导,令导数大于等于0在x>0上恒成立即可.
(2)将a的值代入整理成方程的形式,然后转化为函数考虑其图象与x轴的交点的问题.
试题解析:
(1)f′(x)=﹣![]() ,(x>0)
,(x>0)
依题意f'(x)≥0在x>0时恒成立,即ax2+2x﹣1≤0在x>0恒成立.
则a≤![]() =(
=( ![]() ﹣1)2﹣1在x>0恒成立,
﹣1)2﹣1在x>0恒成立,
即a≤((![]() ﹣1)2﹣1)min(x>0)
﹣1)2﹣1)min(x>0)
当x=1时,(![]() ﹣1)2﹣1取最小值﹣1,
﹣1)2﹣1取最小值﹣1,
∴a的取值范围是(﹣∞,﹣1].
(2)a=﹣![]() ,f(x)=﹣
,f(x)=﹣![]() x+b,
x+b,
∴![]() x2﹣
x2﹣![]() x+lnx﹣b=0
x+lnx﹣b=0
设g(x)=![]() x2﹣
x2﹣![]() x+lnx﹣b(x>0)则g'(x)=
x+lnx﹣b(x>0)则g'(x)=![]() ,
,
列表:
X | (0,1) | 1 | (1,2) | 2 | (2,4) |
g′(x) | + | 0 | ﹣ | 0 | + |
g(x) | ↑ | 极大值 | ↓ | 极小值 | ↑ |
∴g(x)极小值=g(2)=ln2﹣b﹣2,g(x)极大值=g(1)=﹣b﹣![]() ,
,
又g(4)=2ln2﹣b﹣2
∵方程g(x)=0在[1,4]上恰有两个不相等的实数根.
则  ,得:ln2﹣2<b≤﹣
,得:ln2﹣2<b≤﹣![]() .
.


科目:高中数学 来源: 题型:
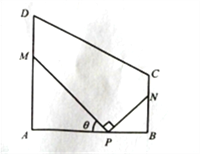
【题目】某地方政府要将一块如图所示的直角梯形ABCD空地改建为健身娱乐广场.已知AD//BC, ![]() 百米,
百米, ![]() 百米,广场入口P在AB上,且
百米,广场入口P在AB上,且![]() ,根据规划,过点P铺设两条相互垂直的笔直小路PM,PN(小路的宽度不计),点M,N分别在边AD,BC上(包含端点),
,根据规划,过点P铺设两条相互垂直的笔直小路PM,PN(小路的宽度不计),点M,N分别在边AD,BC上(包含端点),![]() 区域拟建为跳舞健身广场,
区域拟建为跳舞健身广场, ![]() 区域拟建为儿童乐园,其它区域铺设绿化草坪,设
区域拟建为儿童乐园,其它区域铺设绿化草坪,设![]() .
.
(1)求绿化草坪面积的最大值;
(2)现拟将两条小路PNM,PN进行不同风格的美化,PM小路的美化费用为每百米1万元,PN小路的美化费用为每百米2万元,试确定M,N的位置,使得小路PM,PN的美化总费用最低,并求出最小费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网购已经成为一种时尚,商家为了鼓励消费,购买时在店铺领取优惠券,买后给予好评返还现金等促销手段.经统计,近五年某店铺用于促销的费用![]() (万元)与当年度该店铺的销售收人
(万元)与当年度该店铺的销售收人![]() (万元)的数据如下表:
(万元)的数据如下表:
年份 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 |
促销费用 |
|
|
|
|
|
销售收入 |
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出/span>![]() 关于
关于![]() 的线性回归方
的线性回归方![]() ;
;
(2)2018年度该店铺预测销售收人至少达到![]() 万元,则该店铺至少准备投入多少万元的促销费?
万元,则该店铺至少准备投入多少万元的促销费?
参考公式: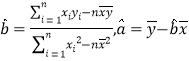
参考数据: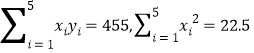
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 两个小岛相距
两个小岛相距![]() 海里,
海里,![]() 岛在
岛在![]() 岛的正南方,现在甲船从
岛的正南方,现在甲船从![]() 岛出发,以
岛出发,以![]() 海里/时的速度向
海里/时的速度向![]() 岛行驶,而乙船同时以
岛行驶,而乙船同时以![]() 海里/时的速度离开
海里/时的速度离开![]() 岛向南偏东
岛向南偏东![]() 方向行驶,行驶多少时间后,两船相距最近?并求出两船的最近距离.
方向行驶,行驶多少时间后,两船相距最近?并求出两船的最近距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 是单调递增函数,求实数
是单调递增函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有两个实数根
内有两个实数根![]() ,记
,记![]() ,求实数
,求实数![]() 的取值范围 .
的取值范围 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表。
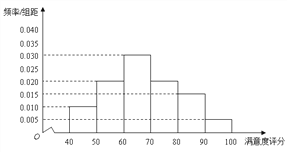
A地区用户满意度评分的频率分布直方图

B地区用户满意度评分的频数分布表
(Ⅰ)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
估计哪个地区的满意度等级为不满意的概率大?说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com