
已知点F1、F2分别是椭圆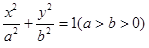 的左、右焦点,A、B是以O(O
的左、右焦点,A、B是以O(O
为坐标原点)为圆心、|OF1|为半径的圆与该椭圆左半部分的两个交点,且△F2AB是正三角形,则此椭圆的离心率为( )
A. B.
B. C.
C.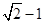 D.
D.
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com