
在平面直角坐标系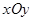 中,已知椭圆
中,已知椭圆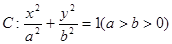 的左焦点为
的左焦点为 ,且椭圆
,且椭圆 的离心率
的离心率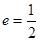 .
.
(1)求椭圆 的方程;
的方程;
(2)设椭圆 的上下顶点分别为
的上下顶点分别为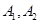 ,
,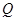 是椭圆
是椭圆 上异于
上异于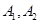 的任一点,直线
的任一点,直线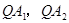 分别交
分别交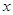 轴于点
轴于点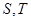 ,证明:
,证明: 为定值,并求出该定值;
为定值,并求出该定值;
(3)在椭圆 上,是否存在点
上,是否存在点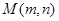 ,使得直线
,使得直线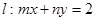 与圆
与圆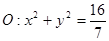 相交于不同的两点
相交于不同的两点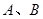 ,且
,且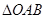 的面积最大?若存在,求出点
的面积最大?若存在,求出点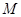 的坐标及对应的
的坐标及对应的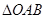 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
(1) 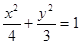 ; (2)定值是4,详见解析;
; (2)定值是4,详见解析;
(3)存在, 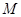 的坐标为
的坐标为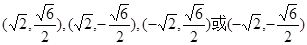 ,
,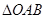 的面积为
的面积为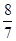 .
.
解析试题分析:(1)根据椭圆的焦点、离心率和 的关系求出椭圆标准方程中的
的关系求出椭圆标准方程中的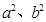 ;(2)先设
;(2)先设 ,求出直线
,求出直线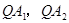 的方程,并求出它们与
的方程,并求出它们与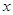 轴的交点
轴的交点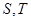 的坐标,建立
的坐标,建立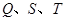 三点坐标的关系,然后利用
三点坐标的关系,然后利用 在椭圆上,从而把
在椭圆上,从而把 中的
中的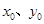 消去得到定值; (3)先假设存在点
消去得到定值; (3)先假设存在点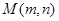 ,则有直线
,则有直线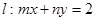 与圆
与圆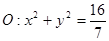 相交,进而写出
相交,进而写出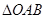 的面积函数,发现利用基本不等式可以求出函数的最大值,故假设存在,再求出取得最大值时点
的面积函数,发现利用基本不等式可以求出函数的最大值,故假设存在,再求出取得最大值时点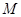 的坐标.
的坐标.
试题解析:解:(1)由题意: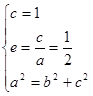 ,解得:
,解得: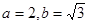 3分
3分
所以椭圆
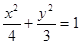 4分
4分
(2) 由(1)可知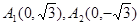 ,设
,设 ,
,
直线 :
: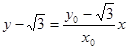 ,令
,令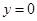 ,得
,得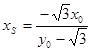 ; 5分
; 5分
直线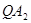 :
: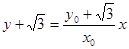 ,令
,令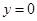 ,得
,得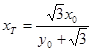 ; 6分
; 6分
则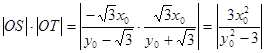 , 7分
, 7分
而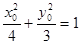 ,所以
,所以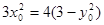 ,
,
所以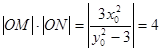 8分
8分
(3)假设存在点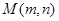 满足题意,则
满足题意,则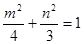 ,即
,即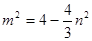
设圆心到直线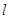 的距离为
的距离为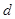 ,则
,则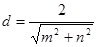 ,且
,且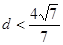 9分
9分
所以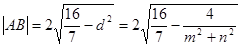 10分
10分
所以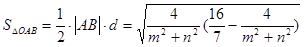 11分
11分
因为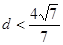 ,所以
,所以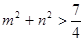 ,所以
,所以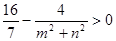
所以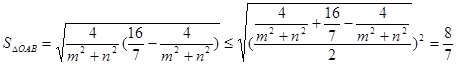 12分
12分
当且仅当 ,即
,即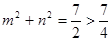 时,
时,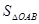 取得最大值
取得最大值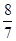
由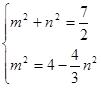 ,解得
,解得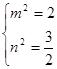 13分
13分
所以存在点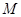 满足题意,点
满足题意,点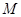 的坐标为
的坐标为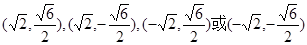
此时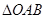 的面积为
的面积为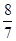 14分
14分
考点:1、椭圆的标准方程,、2解析法,3、直线与圆相交问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
已知椭圆C: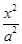 +
+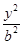 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为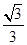 ,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为
,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为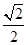 .
.
(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有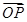 =
=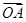 +
+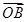 成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.
成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆C: 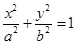 (a>b>0)的两个焦点和短轴的两个端点都在圆
(a>b>0)的两个焦点和短轴的两个端点都在圆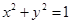 上.
上.
(I)求椭圆C的方程;
(II)若斜率为k的直线过点M(2,0),且与椭圆C相交于A, B两点.试探讨k为何值时,三角形OAB为直角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆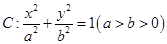 的左右焦点分别为
的左右焦点分别为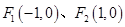 ,且经过点
,且经过点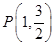 ,
,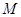 为椭圆上的动点,以
为椭圆上的动点,以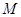 为圆心,
为圆心,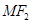 为半径作圆
为半径作圆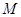 .
.
(1)求椭圆 的方程;
的方程;
(2)若圆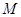 与
与 轴有两个交点,求点
轴有两个交点,求点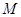 横坐标的取值范围.
横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知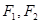 为椭圆
为椭圆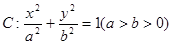 的左,右焦点,
的左,右焦点,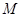 为椭圆上的动点,且
为椭圆上的动点,且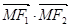 的最大值为1,最小值为-2.
的最大值为1,最小值为-2.
(I)求椭圆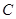 的方程;
的方程;
(II)过点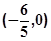 作不与
作不与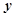 轴垂直的直线
轴垂直的直线 交该椭圆于
交该椭圆于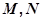 两点,
两点,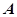 为椭圆的左顶点。试判断
为椭圆的左顶点。试判断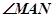 的大小是否为定值,并说明理由.
的大小是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
椭圆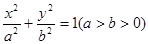 的左、右焦点分别为F1(-1,0),F2(1,0),过F1作与x轴不重合的直线l交椭圆于A,B两点.
的左、右焦点分别为F1(-1,0),F2(1,0),过F1作与x轴不重合的直线l交椭圆于A,B两点.
(Ⅰ)若ΔABF2为正三角形,求椭圆的离心率;
(Ⅱ)若椭圆的离心率满足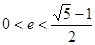 ,0为坐标原点,求证
,0为坐标原点,求证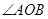 为钝角.
为钝角.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知焦点在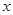 轴上的椭圆
轴上的椭圆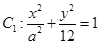 和双曲线
和双曲线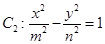 的离心率互为倒数,它们在第一象限交点的坐标为
的离心率互为倒数,它们在第一象限交点的坐标为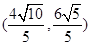 ,设直线
,设直线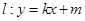 (其中
(其中 为整数).
为整数).
(1)试求椭圆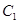 和双曲线
和双曲线 的标准方程;
的标准方程;
(2)若直线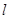 与椭圆
与椭圆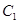 交于不同两点
交于不同两点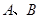 ,与双曲线
,与双曲线 交于不同两点
交于不同两点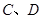 ,问是否存在直线
,问是否存在直线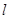 ,使得向量
,使得向量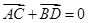 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在直角坐标系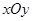 中,曲线
中,曲线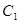 的参数方程为
的参数方程为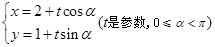 ,
,
以原点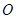 为极点,
为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线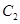 的极坐标方程为
的极坐标方程为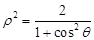 .
.
⑴ 求曲线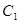 的普通方程和曲线
的普通方程和曲线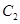 的直角坐标方程;
的直角坐标方程;
⑵ 当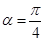 时,曲线
时,曲线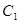 和
和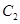 相交于
相交于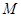 、
、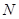 两点,求以线段
两点,求以线段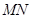 为直径的圆的直角坐标方程.
为直径的圆的直角坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com