
分析 根据题意,由-2∈A分3种情况进行讨论:①、-2=a-1,②、-2=2a2+5a+1,③、-2=a2+1,求出a的值,进而利用集合元素的互异性进行分析,综合即可得答案.
解答 解:根据题意,A={a-1,2a2+5a+1,a2+1},
若-2∈A,则分3种情况进行讨论:
①、-2=a-1,即a=-1,此时集合A元素为-2,-2,2,不满足集合元素的互异性,不符合题意,
②、-2=2a2+5a+1,解可得a=-1或a=-$\frac{3}{2}$,
a=-$\frac{3}{2}$时,此时集合A元素为-$\frac{5}{2}$,-2,$\frac{13}{4}$,符合题意,
由①可得,a=-1不符合题意;
③、-2=a2+1,无解,
综合可得:a=-$\frac{3}{2}$.
点评 本题考查集合元素的特点,关键是利用集合中元素的互异性进行分类讨论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
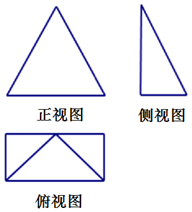 一个空间几何体的三视图如右图,其中正视图是边长为2的正三角形,俯视图是边长分别为1,2的矩形,则该几何体的侧面积为4+$\sqrt{3}$.
一个空间几何体的三视图如右图,其中正视图是边长为2的正三角形,俯视图是边长分别为1,2的矩形,则该几何体的侧面积为4+$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,9) | B. | [-1,9) | C. | [0,9) | D. | (0,9) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 计算小于100的奇数的连乘积 | |
| B. | 计算从1开始的连续奇数的连乘积 | |
| C. | 从1开始的连续奇数的连乘积,当乘积大于100时,计算奇数的个数 | |
| D. | 计算1×3×5×…×n≥100时的最小的n值. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | -4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com