考点:命题的真假判断与应用
专题:综合题,等差数列与等比数列
分析:根据“等方差数列”的定义,我们逐一判断可得答案.
解答:
解:∵{an}是等方差数列,∴an2-an-12=p(p为常数)得到{an2}为首项是a12,公差为p的等差数列;
∴{an2}是等差数列,故①正确,②不正确;
数列{(-1)n}中,an2-an-12=[(-1)n]2-[(-1)n-1]2=0,
∴{(-1)n}是等方差数列;故③正确;
数列{an}中的项列举出来是,a1,a2,…,ak,…,a2k,…
数列{akn}中的项列举出来是,ak,a2k,…,a3k,…,
∵(ak+12-ak2)=(ak+22-ak+12)=(ak+32-ak+22)=…=(a2k2-a2k-12)=p
∴(ak+12-ak2)+(ak+22-ak+12)+(ak+32-ak+22)+…+(a2k2-a2k-12)=kp
∴(akn+12-akn2)=kp
∴{akn}(k∈N*,k为常数)是等方差数列;故④正确.
故答案为:①③④.
点评:此题考查学生灵活运用等差数列的性质及新定义等方差数列化简求值,是一道中档题.



 阅读快车系列答案
阅读快车系列答案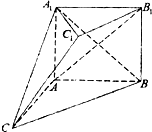 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=