
| A. | (2,4] | B. | (-∞,0]∪[4,+∞) | C. | [4,+∞) | D. | (2,+∞) |
分析 利用分段函数,分析出m的范围,然后利用数形结合求解选项即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}\sqrt{1-{x^2}},x≤1\\-{x^2}+2mx-2m+1,x>1\end{array}$,可知x≤1时,函数是圆的上半部分,函数的最大值为1,
x>1时,f(x)=-x2+2mx-2m+1,的对称轴为x=m,开口向下,对于任意实数a∈(0,1)关于x的方程f(x)-a=0都有四个不相等的实根x1,x2,x3,x4,则x>1时,函数的最大值中的最小值为1,此时m≥2,
在平面直角坐标系中,画出函数y=f(x)与y=a的图象如图: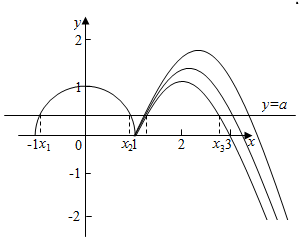
x1+x2=0,x3+x4≥2m≥4,
则x1+x2+x3+x4的取值范围是[4,+∞).
故选:C.
点评 本题考查分段函数的应用,考查函数与方程的应用,函数的图象,以及分析问题解决问题的能力,是难度比较大的题目.


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:高中数学 来源: 题型:选择题
| A. | n+(n+1)+(n+2)+…+(2n-1)=n2 | B. | n+(n+1)+(n+2)+…+(2n-1)=(2n-1)2 | ||
| C. | n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2 | D. | n+(n+1)+(n+2)+…+(3n-1)=(2n-1)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
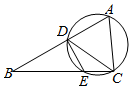 如图,△ABC的边AB、BC与⊙O交于A、D、E、C四点,且AC=BE,∠ADC=∠BDE.
如图,△ABC的边AB、BC与⊙O交于A、D、E、C四点,且AC=BE,∠ADC=∠BDE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
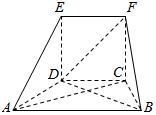 如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AC=$\sqrt{3}$,AB=2BC=2,AC⊥FB.
如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AC=$\sqrt{3}$,AB=2BC=2,AC⊥FB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com