
分析 构造函数,确定其单调性,求出函数的最值,即可确定实数a的取值范围.
解答 解:由题意,f(x)=$\frac{1}{x+\frac{16}{x}}$,而x+$\frac{16}{x}$在(0,3]上单调递减,∴f(x)max=$\frac{1}{3+\frac{16}{3}}$=$\frac{3}{25}$;
g(x)=$\frac{{x}^{2}+2}{x}$=x+$\frac{2}{x}$在(0,3]上单调递减,∴g(x)min=3+$\frac{2}{3}$=$\frac{11}{3}$,
∵关于x的不等式$\frac{x}{{x}^{2}+16}$≤a≤$\frac{{x}^{2}+2}{x}$,对任意x∈(0,3]均成立,
∴实数a的取值范围为$\frac{3}{25}$≤a≤$\frac{11}{3}$,
故答案为:$\frac{3}{25}$≤a≤$\frac{11}{3}$.
点评 本题考查恒成立问题,考查函数的最值,考查学生分析解决问题的能力,正确求最值是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 7.5 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
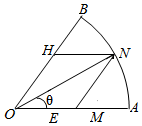 某房地产开发商为吸引更多的消费者购房,决定在一块闲置的扇形空地中修建一个花园,如图,已知扇形AOB的圆心角∠AOB=$\frac{π}{4}$,半径为R,现欲修建的花园为平行四边形OMNH,其中M,H分别在OA,OB上,N在AB上,设∠MON=θ,平行四边形OMNH的面积为S.
某房地产开发商为吸引更多的消费者购房,决定在一块闲置的扇形空地中修建一个花园,如图,已知扇形AOB的圆心角∠AOB=$\frac{π}{4}$,半径为R,现欲修建的花园为平行四边形OMNH,其中M,H分别在OA,OB上,N在AB上,设∠MON=θ,平行四边形OMNH的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2}{3}$) | B. | ($\frac{2}{3}$,+∞) | C. | (0,$\frac{2}{3}$] | D. | [$\frac{2}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{4}$) | B. | (-∞,$\frac{1}{4}$) | C. | (0,$\frac{1}{4}$] | D. | (-∞,$\frac{1}{4}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com