Question

4．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的焦距为2c，以右顶点为圆心，以c为半径的圆与双曲线右支的交点横坐标为$\frac{3}{2}$a，则该双曲线的离心率为（　　）

• A． $\sqrt{2}$
• B． $\sqrt{6}$
• C． 3
• D． 2

Answer 1

分析 利用垂径定理计算交点纵坐标，把交点坐标代入双曲线方程得出a，b，c的关系，从而得出离心率e=$\frac{c}{a}$的大小/

解答 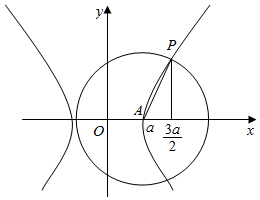解：设双曲线的右顶点为A，双曲线与圆在第一象限内的交点为P，则PA=c，
∴P点纵坐标为$\sqrt{{c}^{2}-\frac{{a}^{2}}{4}}$，
把P（$\frac{3a}{2}$，$\sqrt{{c}^{2}-\frac{{a}^{2}}{4}}$）代入双曲线方程得：$\frac{9}{4}$-$\frac{{c}^{2}-\frac{{a}^{2}}{4}}{{b}^{2}}$=1．
∵b²=c²-a²，∴$\frac{{c}^{2}-\frac{{a}^{2}}{4}}{{c}^{2}-{a}^{2}}$=$\frac{5}{4}$，化简得c=2a．
∴离心率e=$\frac{c}{a}$=2．
故选：D．

点评 本题考查了双曲线的性质，直线与圆的位置关系，属于中档题．