考点:等比数列的通项公式,向量加减混合运算及其几何意义
专题:点列、递归数列与数学归纳法,平面向量及应用
分析:由于点列{A
n}满足:|
|=1,|
|=2|
|+1,设
an=||,则a
1=1,a
n+1=2a
n+1,变形为a
n+1+1=2(a
n+1),可知;数列{a
n+1}是等比数列,利用通项公式可得
an=2n-1.由于A
i均在坐标轴上(i∈N
*),且A
4n-3,A
4n-2,A
4n-1,A
4n,(n∈N
*)分别在y轴的正半轴,x轴的正半轴,y轴的负半轴,x轴的负半轴.
可得向量
+
+…+
的横坐标=a
2-a
4+a
6-a
8+…+a
2010-a
2012+a
2014,向量
+
+…+
的纵坐标=a
1-a
3+a
5-a
7+…+-a
2011+a
2013,再利用等比数列的前n项和公式即可得出.
解答:
解:∵点列{A
n}满足:|
|=1,|
|=2|
|+1,
设
an=||,则a
1=1,a
n+1=2a
n+1,化为a
n+1+1=2(a
n+1),
∴数列{a
n+1}是等比数列,
∴
an+1=(a1+1)•2n-1=2
n.
∴
an=2n-1.
由于A
i均在坐标轴上(i∈N
*),
且A
4n-3,A
4n-2,A
4n-1,A
4n,分别在y轴的正半轴,x轴的正半轴,y轴的负半轴,x轴的负半轴.
∴向量
+
+…+
的横坐标=a
2-a
4+a
6-a
8+…+a
2010-a
2012+a
2014=(2
2-1)-(2
4-1)+(2
6-1)-(2
8-1)+…+(2
2010-1)-(2
2012-1)+(2
2014-1)
=2
2-2
4+2
6-2
8+…+2
2010-2
2012+2
2014-1
=
-1
=
.
同理可得向量
+
+…+
的纵坐标=a
1-a
3+a
5-a
7+…+-a
2011+a
2013=
.
∴向量
+
+…+
=
(,).
故选:D.
点评:本题考查了等比数列的通项公式、前n项和公式、向量的运算等基础知识与基本技能方法,考查了分类讨论和数形结合的思想方法,考查了推理能力和计算能力,属于难题.

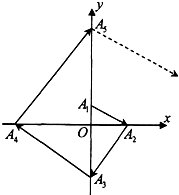 如图所示,点列{An}满足:|
如图所示,点列{An}满足:|

 阅读快车系列答案
阅读快车系列答案