
| A. | 3或-1 | B. | 9或1 | C. | 1 | D. | 9 |
分析 设正项的等比数列{an}的公比为q>0,由3a1,$\frac{1}{2}{a_3}$,2a2成等差数列,可得${a}_{1}{q}^{2}$=3a1+2a1q,解得q,再利用通项公式即可得出.
解答 解:设正项的等比数列{an}的公比为q>0,∵3a1,$\frac{1}{2}{a_3}$,2a2成等差数列,
∴a3=3a1+2a2,
∴${a}_{1}{q}^{2}$=3a1+2a1q,
化为q2-2q-3=0,
解得q=3.
则$\frac{{{a_{2014}}+{a_{2015}}}}{{{a_{2012}}+{a_{2013}}}}$=$\frac{{a}_{2012}({q}^{2}+{q}^{3})}{{a}_{2012}(1+q)}$=q2=9,
故选:D.
点评 本题考查了等比数列的通项公式、递推关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| X | -1 | 0 | 1 |
| P | a | b | c |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
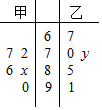 一次数学考试后,某老师从自己带的两个班级中各抽取5人,记录他们的考试成绩,得到如图所示的茎叶图,已知甲班5名同学成绩的平均数为81,乙班5名同学的中位数为73,则x-y的值为( )
一次数学考试后,某老师从自己带的两个班级中各抽取5人,记录他们的考试成绩,得到如图所示的茎叶图,已知甲班5名同学成绩的平均数为81,乙班5名同学的中位数为73,则x-y的值为( )| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∉R,x2≠x | B. | ?x∈R,x2=x | C. | ?x0∈R,x${\;}_{0}^{2}$≠x0 | D. | ?x0∈R,x${\;}_{0}^{2}$=x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com